Page 247 - Fisika Terapan for Engineers and Scientists

14.4 Elasticity of Materials 447

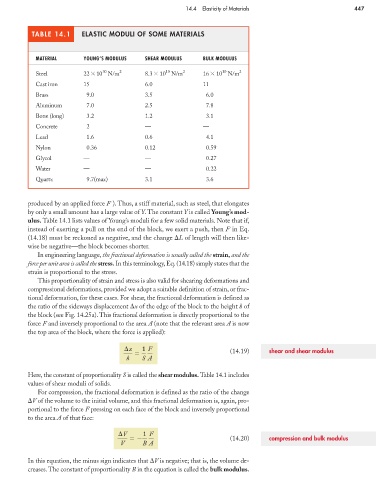
TABLE 14.1 ELASTIC MODULI OF SOME MATERIALS

MATERIAL YOUNG’S MODULUS SHEAR MODULUS BULK MODULUS

10 2 10 2 10 2
Steel 22 10 N/m 8.3 10 N/m 16 10 N/m
Cast iron 15 6.0 11
Brass 9.0 3.5 6.0
Aluminum 7.0 2.5 7.8
Bone (long) 3.2 1.2 3.1
Concrete 2 — —
Lead 1.6 0.6 4.1
Nylon 0.36 0.12 0.59
Glycol — — 0.27
Water — — 0.22
Quartz 9.7(max) 3.1 3.6

produced by an applied force F ). Thus, a stiff material, such as steel, that elongates
by only a small amount has a large value of Y.The constant Y is called Young’s mod-
ulus. Table 14.1 lists values of Young’s moduli for a few solid materials. Note that if,
instead of exerting a pull on the end of the block, we exert a push, then F in Eq.
(14.18) must be reckoned as negative, and the change L of length will then like-
wise be negative—the block becomes shorter.
In engineering language, the fractional deformation is usually called the strain, and the
force per unit area is called the stress. In this terminology,Eq.(14.18) simply states that the
strain is proportional to the stress.
This proportionality of strain and stress is also valid for shearing deformations and
compressional deformations, provided we adopt a suitable definition of strain, or frac-
tional deformation, for these cases. For shear, the fractional deformation is defined as
the ratio of the sideways displacement x of the edge of the block to the height h of
the block (see Fig. 14.25a).This fractional deformation is directly proportional to the
force F and inversely proportional to the area A (note that the relevant area A is now
the top area of the block, where the force is applied):

¢x 1 F shear and shear modulus
(14.19)
h S A

Here, the constant of proportionality S is called the shear modulus. Table 14.1 includes
values of shear moduli of solids.
For compression, the fractional deformation is defined as the ratio of the change
V of the volume to the initial volume, and this fractional deformation is, again, pro-
portional to the force F pressing on each face of the block and inversely proportional
to the area A of that face:

¢V 1 F
(14.20) compression and bulk modulus
V B A

In this equation, the minus sign indicates that V is negative; that is, the volume de-
creases.The constant of proportionality B in the equation is called the bulk modulus.