Page 79 - Cardiac Nursing

6/3
0/2
6/3
0
0
1
1
009
0/2
009
68.
q
68.
2-0
2-0
xd
0
xd
q
q
5:3
p
p
5 A
e 5
5 A
r
r
ta
p
ta
Pa
Pa
3
5:3
3
g
e 5
g
Pa
g
0-c
K34
K34
02_
02_
0-c
LWB
04
LWBK340-c02_ p pp042-068.qxd 06/30/2009 15:33 Page 55 Aptara a a
04
LWB
p
C HAPTER 2 / Systemic and Pulmonary Circulation and Oxygen Delivery 55
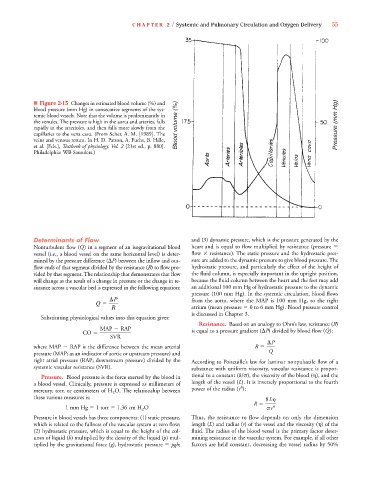
■ Figure 2-15 Changes in estimated blood volume (%) and
blood pressure (mm Hg) in consecutive segments of the sys-
temic blood vessels. Note that the volume is predominantly in
the venules. The pressure is high in the aorta and arteries, falls
rapidly in the arterioles, and then falls more slowly from the
capillaries to the vena cava. (From Scher, A. M. [1989]. The
veins and venous return. In H. D. Patton, A. Fuchs, B. Hille,
et al. [Eds.], Textbook of physiology, Vol. 2 [21st ed., p. 880].
Philadelphia: WB Saunders.)
Determinants of Flow and (3) dynamic pressure, which is the pressure generated by the
˙
Nonturbulent flow (Q) in a segment of an isogravitational blood heart and is equal to flow multiplied by resistance (pressure
vessel (i.e., a blood vessel on the same horizontal level) is deter- flow resistance). The static pressure and the hydrostatic pres-
P
mined by the pressure difference ( P) between the inflow and out-P sure are added to the dynamic pressure to give blood pressure. The
R
R
flow ends of that segment divided by the resistance (R) to flow pro- hydrostatic pressure, and particularly the effect of the height of
vided by that segment. The relationship that demonstrates that flow the fluid column, is especially important in the upright position,
will change as the result of a change in pressure or the change in re- because the fluid column between the heart and the feet may add
sistance across a vascular bed is expressed in the following equation: an additional 100 mm Hg of hydrostatic pressure to the dynamic
pressure (100 mm Hg). In the systemic circulation, blood flows
# ¢P from the aorta, where the MAP is 100 mm Hg, to the right
Q
R atrium (mean pressure 0 to 6 mm Hg). Blood pressure control
is discussed in Chapter 3.
Substituting physiological values into this equation gives:
Resistance. Based on an analogy to Ohm’s law, resistance (R)
R
R
MAP RAP ˙
P
P
CO is equal to a pressure gradient ( P) divided by blood flow (Q):
SVR
¢P
where MAP RAP is the difference between the mean arterial R #
pressure (MAP; as an indicator of aortic or upstream pressure) and Q
right atrial pressure (RAP; downstream pressure) divided by the According to Poiseuille’s law for laminar nonpulsatile flow of a
systemic vascular resistance (SVR). substance with uniform viscosity, vascular resistance is propor-
Pressure. Blood pressure is the force exerted by the blood in tional to a constant (8/ ), the viscosity of the blood ( ), and the
a blood vessel. Clinically, pressure is expressed as millimeters of length of the vessel (L). It is inversely proportional to the fourth
4
r
mercury, torr, or centimeters of H 2 O. The relationship between power of the radius (r ):
these various measures is: 8Lh
R
1 mm Hg 1 torr 1.36 cm H 2 O pr 4
Pressure in blood vessels has three components: (1) static pressure, Thus, the resistance to flow depends on only the dimension
which is related to the fullness of the vascular system at zero flow; length (L) and radius (r) of the vessel and the viscosity ( ) of the
r
(2) hydrostatic pressure, which is equal to the height of the col- fluid. The radius of the blood vessel is the primary factor deter-
umn of liquid (h) multiplied by the density of the liquid (p) mul- mining resistance in the vascular system. For example, if all other
(
(
(
g
tiplied by the gravitational force (g), hydrostatic pressure pgh; factors are held constant, decreasing the vessel radius by 50%
g