Page 233 - 9780077418427.pdf

/Users/user-f465/Desktop
tiL12214_ch08_203-228.indd Page 210 9/1/10 9:45 PM user-f465
tiL12214_ch08_203-228.indd Page 210 9/1/10 9:45 PM user-f465 /Users/user-f465/Desktop

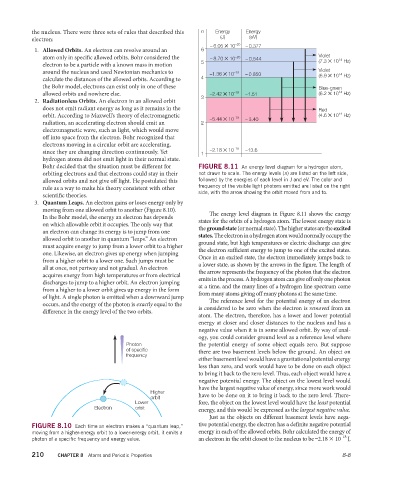
the nucleus. There were three sets of rules that described this n Energy Energy
electron: (J) (eV)
– 6.05 ✕ 10 –20 – 0.377
1. Allowed Orbits. An electron can revolve around an 6
Violet

atom only in specific allowed orbits. Bohr considered the 5 – 8.70 ✕ 10 –20 – 0.544 (7.3 ✕ 10 Hz)
14
electron to be a particle with a known mass in motion
Violet
around the nucleus and used Newtonian mechanics to –1.36 ✕ 10 –19 – 0.850 (6.9 ✕ 10 Hz)
14
calculate the distances of the allowed orbits. According to 4
the Bohr model, electrons can exist only in one of these Blue-green
14
allowed orbits and nowhere else. 3 –2.42 ✕ 10 –19 –1.51 (6.2 ✕ 10 Hz)
2. Radiationless Orbits. An electron in an allowed orbit
does not emit radiant energy as long as it remains in the Red
14
orbit. According to Maxwell’s theory of electromagnetic –5.44 ✕ 10 –19 – 3.40 (4.6 ✕ 10 Hz)
radiation, an accelerating electron should emit an 2
electromagnetic wave, such as light, which would move

off into space from the electron. Bohr recognized that
electrons moving in a circular orbit are accelerating,
–2.18 ✕ 10 –18 –13.6
since they are changing direction continuously. Yet 1
hydrogen atoms did not emit light in their normal state.
Bohr decided that the situation must be diff erent for FIGURE 8.11 An energy level diagram for a hydrogen atom,
orbiting electrons and that electrons could stay in their not drawn to scale. The energy levels (n) are listed on the left side,

allowed orbits and not give off light. He postulated this followed by the energies of each level in J and eV. The color and
rule as a way to make his theory consistent with other frequency of the visible light photons emitted are listed on the right
side, with the arrow showing the orbit moved from and to.
scientifi c theories.
3. Quantum Leaps. An electron gains or loses energy only by
moving from one allowed orbit to another (Figure 8.10).
The energy level diagram in Figure 8.11 shows the energy
In the Bohr model, the energy an electron has depends
states for the orbits of a hydrogen atom. The lowest energy state is

on which allowable orbit it occupies. The only way that
the ground state (or normal state). The higher states are the excited
an electron can change its energy is to jump from one
states. The electron in a hydrogen atom would normally occupy the
allowed orbit to another in quantum “leaps.” An electron
ground state, but high temperatures or electric discharge can give
must acquire energy to jump from a lower orbit to a higher
the electron sufficient energy to jump to one of the excited states.
one. Likewise, an electron gives up energy when jumping
Once in an excited state, the electron immediately jumps back to
from a higher orbit to a lower one. Such jumps must be
a lower state, as shown by the arrows in the figure. The length of
all at once, not partway and not gradual. An electron
the arrow represents the frequency of the photon that the electron
acquires energy from high temperatures or from electrical
emits in the process. A hydrogen atom can give off only one photon
discharges to jump to a higher orbit. An electron jumping
at a time, and the many lines of a hydrogen line spectrum come
from a higher to a lower orbit gives up energy in the form
from many atoms giving off many photons at the same time.
of light. A single photon is emitted when a downward jump
The reference level for the potential energy of an electron
occurs, and the energy of the photon is exactly equal to the
is considered to be zero when the electron is removed from an
difference in the energy level of the two orbits.

atom. The electron, therefore, has a lower and lower potential
energy at closer and closer distances to the nucleus and has a
negative value when it is in some allowed orbit. By way of anal-
ogy, you could consider ground level as a reference level where
Photon the potential energy of some object equals zero. But suppose
of specific there are two basement levels below the ground. An object on
frequency
either basement level would have a gravitational potential energy
less than zero, and work would have to be done on each object
to bring it back to the zero level. Thus, each object would have a
negative potential energy. The object on the lowest level would
have the largest negative value of energy, since more work would
Higher
orbit have to be done on it to bring it back to the zero level. There-
Lower fore, the object on the lowest level would have the least potential
Electron orbit energy, and this would be expressed as the largest negative value.
Just as the objects on different basement levels have nega-
tive potential energy, the electron has a definite negative potential
FIGURE 8.10 Each time an electron makes a “quantum leap,”
moving from a higher-energy orbit to a lower-energy orbit, it emits a energy in each of the allowed orbits. Bohr calculated the energy of
–18
photon of a specific frequency and energy value. an electron in the orbit closest to the nucleus to be –2.18 × 10 J,
210 CHAPTER 8 Atoms and Periodic Properties 8-8