Page 423 - Buku Materi Pembelajaran Rangkaian Listrik II dan Praktikum
P. 423
Penyelesaian:
Berdasarkan persamaan [10.7], frekuensi resonansi f0 dari rangkaian
gambar 10.6 adalah:
−6
2
1 (1 )(10 ) 10 5
f = √(1 − ) = √1 − 0,99
0
−6
2π√(10 )(10 ) 10 −4 2π
−4
= 15,8 kHz
2.3 Band Pass Filter
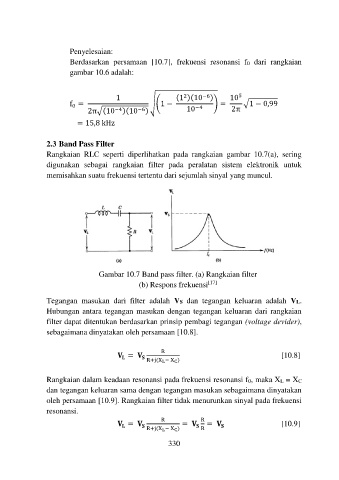
Rangkaian RLC seperti diperlihatkan pada rangkaian gambar 10.7(a), sering
digunakan sebagai rangkaian filter pada peralatan sistem elektronik untuk
memisahkan suatu frekuensi tertentu dari sejumlah sinyal yang muncul.
Gambar 10.7 Band pass filter. (a) Rangkaian filter
(b) Respons frekuensi [17]
Tegangan masukan dari filter adalah VS dan tegangan keluaran adalah VL.
Hubungan antara tegangan masukan dengan tegangan keluaran dari rangkaian
filter dapat ditentukan berdasarkan prinsip pembagi tegangan (voltage devider),
sebagaimana dinyatakan oleh persamaan [10.8].
R
= [10.8]
R+j(X L − X C )
Rangkaian dalam keadaan resonansi pada frekuensi resonansi f0, maka XL = XC
dan tegangan keluaran sama dengan tegangan masukan sebagaimana dinyatakan
oleh persamaan [10.9]. Rangkaian filter tidak menurunkan sinyal pada frekuensi
resonansi.
R R
= = = [10.9]
R+j(X L − X C ) R
330