Page 28 - FOCUS KSSM TG 4 MATEMATIK TAMBAHAN

Matematik Tambahan Tingkatan 4 Jawapan

(a) Graf fungsi f(x) = 5 – 3x – 2x adalah pantulan graf simetrinya menjadi x = 1 dan nilai minimum graf
2
fungsi f(x) = 5 + 3x – 2x pada paksi-y kerana nilai b tidak berubah.
2
telah berubah daripada +3 kepada –3. (iii) Apabila k berubah dari 5 ke – 1, bentuk graf tidak
(b) Graf fungsi f(x) = –1 + 3x – 2x adalah anjakan tegak berubah tetapi kedudukan graf dianjakkan secara
2
bagi graf f(x) = 5 + 3x – 2x ke bawah paksi-x kerana menegak 6 unit ke bawah. Nilai minimumnya
2
nilai c telah berubah daripada 5 kepada –1. menjadi –1 dan persamaan paksi simetrinya
(c) Graf fungsi f(x) = 2x – 3x – 5 adalah songsangan masih sama, iaitu x = 3.
2
bagi f(x) = 5 + 3x – 2x kerana –(2x – 3x – 5) = 5 + 3
2
2
3x – 2x . Iaitu, graf terbalik. 24. (a) p = – 4, q = – , n = 13
2
2
3. (a) Punca nyata yang sama (b) x = –1
(b) Punca nyata yang berbeza (c) –1
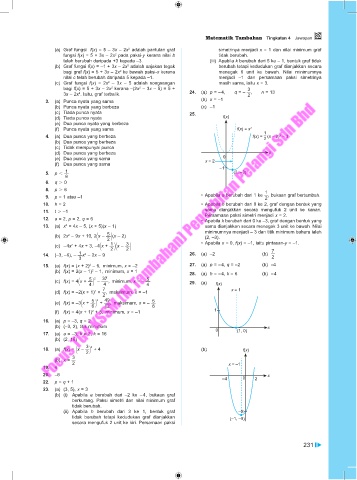
(c) Tiada punca nyata 25.
(d) Tiada punca nyata f(x)
(e) Dua punca nyata yang berbeza
(f) Punca nyata yang sama f(x) = x 2
1
–
4. (a) Dua punca yang berbeza f(x) = (x – 2) – 3
2
2
(b) Dua punca yang berbeza
(c) Tidak mempunyai punca
(d) Dua punca yang berbeza x
(e) Dua punca yang sama x = 2 0
(f) Dua punca yang sama
–1
1

5. p , — (2, –3)
8
6. q . 0
8. p . 6 1
9. p = 1 atau –1 • Apabila a berubah dari 1 ke , bukaan graf bertambah.
2
10. h = 2 • Apabila h berubah dari 0 ke 2, graf dengan bentuk yang
11. t . –1 sama dianjakkan secara mengufuk 2 unit ke kanan.
Persamaan paksi simetri menjadi x = 2.
12. a = 2, p = 2, q = 6
• Apabila k berubah dari 0 ke –3, graf dengan bentuk yang
13. (a) x + 4x – 5, (x + 5)(x – 1) sama dianjakkan secara menegak 3 unit ke bawah. Nilai
2
5
1
(b) 2x – 9x + 10, 2 x – — 2 (x – 2) minimumnya menjadi – 3 dan titik minimum baharu ialah
2
2 (2, –3).
1
3
(c) – 4x + 4x + 3, –4 x + — 21 x – — 2 • Apabila x = 0, f(x) = –1, iaitu pintasan-y = –1.
1
2
2
2
1
14. (–3, –6), – —x – 2x – 9 26. (a) –2 (b) 7
2
3 2
15. (a) f(x) = (x + 2) – 6, minimum, x = –2 27. (a) p = – 4, q = –2 (b) –4
2
2
(b) f(x) = 2(x – 1) – 1, minimum, x = 1 28. (a) h = – 4, k = 6 (b) – 4
5
5
1
(c) f(x) = 4 x + — 2 2 – 37 , minimum, x = – — 29. (a) f(x)
4
4
4
7 x = 1
(d) f(x) = –2(x + 1) + , maksimum, x = –1
2
2
5
5
(e) f(x) = –3 x + — 2 2 + 49 , maksimum, x = – —
1
12
6
6
2
(f) f(x) = 4(x + 1) + 5, minimum, x = –1 1
16. (a) p = –3, q = 2
(b) (–3, 2), titik minimum x
0 (1, 0)
17. (a) a = –3, h = 2, k = 16
(b) (2, 16)
1
2
18. (a) f(x) = x – 3 2 + 4 (b) f(x)
2
3
(b) x =
2 x = –1
19. 4
20. –6 x
–4 0 2
22. p = q + 1
23. (a) (3, 5), x = 3
(b) (i) Apabila a berubah dari –2 ke – 4, bukaan graf
berkurang. Paksi simetri dan nilai minimum graf
tidak berubah.
(ii) Apabila h berubah dari 3 ke 1, bentuk graf –8
tidak berubah tetapi kedudukan graf dianjakkan (–1, –9)
secara mengufuk 2 unit ke kiri. Persamaan paksi
231