Page 503 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

17.1 REGRESIÓN LINEAL 479

donde a y b son constantes. Este modelo se emplea en muchos campos de la ingeniería
1
1
para caracterizar cantidades que aumentan (b positivo) o disminuyen (b negativo), a
1
1
una velocidad que es directamente proporcional a sus propias magnitudes. Por ejemplo,
el crecimiento poblacional o el decaimiento radiactivo tienen este comportamiento. Como
≠ 0)
se ilustra en la figura 17.9a, la ecuación representa una relación no lineal (para b 1
entre y y x.
Otro ejemplo de modelo no lineal es la ecuación de potencias
y = a x b2 (17.13)
2
donde a y b son coeficientes constantes. Este modelo tiene muchas aplicaciones en
2
2
todos los campos de la ingeniería. Como se ilustra en la figura 17.9b, la ecuación (para
b ≠ 0 o 1) es no lineal.
2

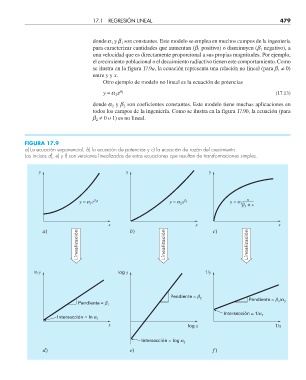
FIGURA 17.9
a) La ecuación exponencial, b) la ecuación de potencias y c) la ecuación de razón del crecimiento.
Los incisos d), e) y f) son versiones linealizadas de estas ecuaciones que resultan de transformaciones simples.

y y y

y = a e b 1 x y = a x b 2 y = a x
1 2 3
b + x
3
x x x
Linealización Linealización Linealización
a) b) c)

ln y log y 1/y

Pendiente = b 2 Pendiente = b /a
Pendiente = b 1 3 3
Intersección = 1/a 3
Intersección = ln a 1
x log x 1/x

Intersección = log a 2
d) e) f )

Chapra-17.indd 479 6/12/06 13:57:15
6/12/06 13:57:15
Chapra-17.indd 479