Page 623 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT5.6 MÉTODOS AVANZADOS Y REFERENCIAS ADICIONALES 599

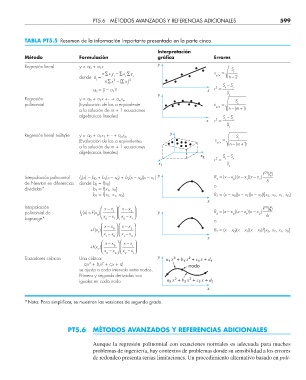
TABLA PT5.5 Resumen de la información importante presentada en la parte cinco.
Interpretación
Método Formulación gráfi ca Errores
y
Regresión lineal y = a 0 + a 1 x S
nx y∑ − ∑ x ∑ y s = r
donde a = ii i i yx/ n− 2
1 nx∑ 2 − ∑( x ) 2
i i S − S
–
2
a 0 = y – a 1 x – x r = t r
y S t
Regresión y = a 0 + a 1 x +···+ a m x m S
polinomial (Evaluación de las a equivalente s yx/ = n ( − r
a la solución de m + 1 ecuaciones m+1 )
algebraicas lineales) S − S
2
x r = t r
S
t
Regresión lineal múltiple y = a 0 + a 1 x 1 +···+ a m x m y S
r
(Evaluación de las a equivalentes s yx/ = n (− m+1 )
a la solución de m + 1 ecuaciones
algebraicas lineales)
x 2 S − S
r = t r
2
x 1 S t
f () ξ
3 ()
Interpolación polinomial f 2 (x) = b 0 + b 1 (x – x 0 ) + b 2 (x – x 0 )(x – x 1 ) y R = ( x − x )( x − x x −)( x ) 6
2
1
2
0
de Newton en diferencias donde b 0 = f(x 0 ) o
divididas* b 1 = f[x 1 , x 0 ]
b 2 = f[x 2 , x 1 , x 0 ] R 2 = (x – x 0 )(x – x 1 )(x – x 2 )f[x 3 , x 2 , x 1 , x 0 ]
x
Interpolación ⎛ x − x ⎞ ⎛ x − x ⎞ f () ξ
3 ()
polinomial de fx() = f x( ) ⎜ 1 ⎟ ⎜ 2 ⎟ y R = ( x − x )( x − x x −)( x )
1
0
2
2
2 0 ⎝ x − x ⎠ ⎝ x − x ⎠ 6
Lagrange* 0 1 0 2 o
⎛ x − x ⎞ ⎛ x − x ⎞
+fx () ⎜ 0 ⎟ ⎜ 2 ⎟ R 2 = (x – x 0 )(x – x 1 )(x – x 2 )f [x 3 , x 2 , x 1 , x 0 ]
1
⎝ x − x ⎠ ⎝ x − x ⎠
0
1
1
2
x
⎛ x − x ⎞ ⎛ x − x ⎞
+fx () ⎜ 0 ⎟ ⎜ 1 ⎟
2
⎝ x 2 − x 0 ⎠ ⎝ x 2 − x 1 ⎠
Trazadores cúbicos Una cúbica: y a x + b x + c x + d 1
3
2
1
1
1
3 2
a i x + b i x + c i x + d i nodo
se ajusta a cada intervalo entre nodos.
Primera y segunda derivadas son 3 2
iguales en cada nodo a x + b x + c x + d 2
2
2
2
x
* Nota: Para simplifi car, se muestran las versiones de segundo grado.
PT5.6 MÉTODOS AVANZADOS Y REFERENCIAS ADICIONALES
Aunque la regresión polinomial con ecuaciones normales es adecuada para muchos
problemas de ingeniería, hay contextos de problemas donde su sensibilidad a los errores
de redondeo presenta serias limitaciones. Un procedimiento alternativo basado en poli-
6/12/06 13:59:04
Chapra-20.indd 599 6/12/06 13:59:04
Chapra-20.indd 599