Page 618 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

594 ESTUDIO DE CASOS: AJUSTE DE CURVAS

Como ingeniero que trabaja para una compañía de infraestructura,
el lector debe pronosticar la población que habrá dentro de 5 años a
fin de anticipar la demanda de energía. Emplee un modelo exponen-
cial y regresión lineal para efectuar dicha predicción.

Ingeniería mecánica/aeroespacial
20.42 Con base en la tabla 20.4, utilice interpolación lineal y
cuadrática para calcular el valor de Q para D = 1.23 ft, y S =
0.001 ft/ft. Compare sus resultados con el mismo valor calcu lado
con la fórmula que se obtuvo en la sección 20.4.
20.43 Reproduzca la sección 20.4, pero desarrolle una ecuación
para predecir la pendiente como función del diámetro y flujo.
Compare sus resultados con los de la fórmula de la sección 20.4
y analice su respuesta.
2
–3
20.44 La viscosidad dinámica del agua m(10 N · s/m ) se rela-
ciona con la temperatura T(°C), de la manera siguiente:
T 0 5 10 20 30 40
m 1.787 1.519 1.307 1.002 0.7975 0.6529
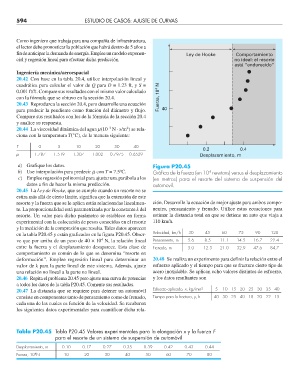
a) Grafique los datos. Figura P20.45
b) Use interpolación para predecir m con T = 7.5ºC. Gráfi ca de la fuerza (en 10 newtons) versus el desplazamiento
4
c) Emplee regresión polinomial para ajustar una parábola a los (en metros) para el resorte del sistema de suspensión del
datos a fin de hacer la misma predicción. automovil.
20.45 La Ley de Hooke, que se cumple cuando un resorte no se
estira más allá de cierto límite, significa que la extensión de este
resorte y la fuerza que se le aplica están relacionadas linealmen- ción. Desarrolle la ecuación de mejor ajuste para ambos compo-
te. La proporcionalidad está parametrizada por la constante k del nentes, pensamiento y frenado. Utilice estas ecuaciones para
resorte. Un valor para dicho parámetro se establece en forma estimar la distancia total en que se detiene un auto que viaja a
experimental con la colocación de pesos conocidos en el resorte 110 km/h.
y la medición de la compresión que resulta. Tales datos aparecen
en la tabla P20.45 y están graficados en la figura P20.45. Obser- Velocidad, km/h 30 45 60 75 90 120
4
ve que por arriba de un peso de 40 × 10 N, la relación lineal Pensamiento, m 5.6 8.5 11.1 14.5 16.7 22.4
entre la fuerza y el desplazamiento desaparece. Esta clase de Frenado, m 5.0 12.3 21.0 32.9 47.6 84.7
comportamiento es común de lo que se denomina “resorte en
deformación”. Emplee regresión lineal para determinar un 20.48 Se realiza un experimento para definir la relación entre el
valor de k para la parte lineal de este sistema. Además, ajuste esfuerzo aplicado y el tiempo para que se fracture cierto tipo de
una relación no lineal a la parte no lineal. acero inoxidable. Se aplican ocho valores distintos de esfuerzo,
20.46 Repita el problema 20.45 pero ajuste una curva de potencias y los datos resultantes son
a todos los datos de la tabla P20.45. Comente sus resultados.
20.47 La distancia que se requiere para detener un automóvil Esfuerzo aplicado, x, kg/mm 2 5 10152025303540
consiste en componentes tanto de pensamiento como de frenado, Tiempo para la fractura, y, h 40 30254018202215
cada una de las cuales es función de la velocidad. Se recabaron
los siguientes datos experimentales para cuantificar dicha rela-

Tabla P20.45 Tabla P20.45 Valores experimentales para la elongación x y la fuerza F
para el resorte de un sistema de suspensión de automóvil
Desplazamiento, m 0.10 0.17 0.27 0.35 0.39 0.42 0.43 0.44
4
Fuerza, 10 N 10 20 30 40 50 60 70 80

6/12/06 13:59:02
Chapra-20.indd 594 6/12/06 13:59:02
Chapra-20.indd 594