Page 627 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

DIFERENCIACIÓN E
INTEGRACIÓN NUMÉRICAS

PT6.1 MOTIVACIÓN

El cálculo es la matemática del cambio. Como los ingenieros deben tratar en forma con-
tinua con sistemas y procesos que cambian, el cálculo es una herramienta esencial en
nuestra profesión. En la esencia del cálculo están dos conceptos matemáticos relaciona-
dos: la diferenciación y la integración.
De acuerdo a la definición del diccionario, diferenciar significa “marcar por dife-
rencias; distinguir;… percibir la diferencia en o entre”. En el contexto de las matemáti-
cas, la derivada sirve como el principal vehículo para la diferenciación, representa la
razón de cambio de una variable dependiente con respecto a una variable independiente.
Como se ilustra en la figura PT6.1, la definición matemática de la derivada empieza con
una aproximación por diferencias:

∆y fx +( ∆x) – ( )
fx
= i i (PT6.1)
∆x ∆x
donde y y f(x) son representaciones alternativas de la variable dependiente y x es la va-
riable independiente. Si se hace que ∆x se aproxime a cero, como sucede en los movi-
mientos mostrados desde la figura PT6.1a a la PT6.1c, el cociente de las diferencias se
convierte en una derivada
fx
dy fx + ∆( i x) – ( )
i
= lím
dx ∆ x→0 ∆ x

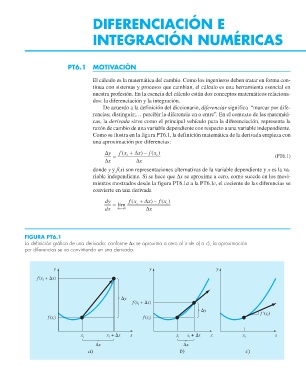
FIGURA PT6.1
La defi nición gráfi ca de una derivada: conforme ∆x se aproxima a cero al ir de a) a c), la aproximación
por diferencias se va convirtiendo en una derivada.

y y y
f(x + x)
i

y
f(x + x)
i
y
f'(x ) i
f(x ) i f(x ) i

x i x + x x x i x + x x x i x
i
i
x x
a) b) c)

6/12/06 13:59:37
Chapra-21.indd 603 6/12/06 13:59:37
Chapra-21.indd 603