Page 630 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

606 DIFERENCIACIÓN E INTEGRACIÓN NUMÉRICAS

litudes como sus diferencias desde una perspectiva numérica. Además, nuestro análisis
tendrá relevancia en las siguientes partes del libro, donde se estudiarán las ecuaciones
diferenciales.

PT6.1.1 Métodos sin computadora para diferenciación
e integración

La función que va a diferenciarse o integrarse estará, usualmente, en una de las siguien-
tes tres formas:

1. Una función continua simple como un polinomio, una función exponencial o una
función trigonométrica.
2. Una función continua complicada que es difícil o imposible de diferenciar o integrar
directamente.
3. Una función tabulada donde los valores de x y f(x) están dados como un conjunto discreto
de puntos, lo cual es el caso cuando se tienen datos experimentales o de campo.

En el primer caso, la derivada o la integral de una función simple se puede evaluar
analíticamente usando el cálculo. En el segundo caso, las soluciones analíticas a menudo
no son fáciles e incluso algunas veces son imposibles de obtener. En tales situaciones, así
como en el tercer caso de datos discretos, se deberán emplear métodos aproximados.
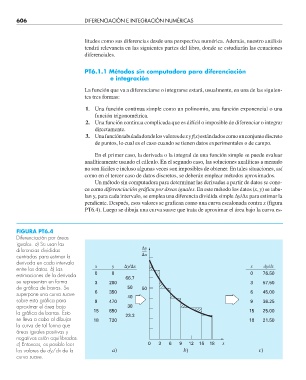
Un método sin computadora para determinar las derivadas a partir de datos se cono-
ce como diferenciación gráfica por áreas iguales. En este método los datos (x, y) se tabu-
lan y, para cada intervalo, se emplea una diferencia dividida simple ∆y/∆x para estimar la
pendiente. Después, esos valores se grafican como una curva escalonada contra x (figura
PT6.4). Luego se dibuja una curva suave que trata de aproximar el área bajo la curva es-

FIGURA PT6.4
Diferenciación por áreas
iguales. a) Se usan las
diferencias divididas y
centradas para estimar la x
derivada en cada intervalo
entre los datos. b) Las x y y/x x dy/dx
estimaciones de la derivada 0 0 66.7 0 76.50
se representan en forma 3 200 3 57.50
de gráfi ca de barras. Se 50 50
superpone una curva suave 6 350 40 6 45.00
sobre esta gráfi ca para 9 470 9 36.25
aproximar el área bajo 30
la gráfi ca de barras. Esto 15 650 23.3 15 25.00
se lleva a cabo al dibujar 18 720 18 21.50
la curva de tal forma que
áreas iguales positivas y
negativas estén equilibradas.
c) Entonces, es posible leer 0 3 6 9 12 15 18 x
los valores de dy/dx de la a) b) c)
curva suave.

6/12/06 13:59:38
Chapra-21.indd 606 6/12/06 13:59:38
Chapra-21.indd 606