Page 631 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT6.1 MOTIVACIÓN 607

f(x)

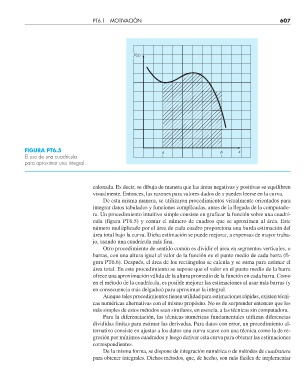
FIGURA PT6.5 a b x
El uso de una cuadrícula
para aproximar una integral.

calonada. Es decir, se dibuja de manera que las áreas negativas y positivas se equilibren
visualmente. Entonces, las razones para valores dados de x pueden leerse en la curva.
De esta misma manera, se utilizaron procedimientos visualmente orientados para
integrar datos tabulados y funciones complicadas, antes de la llegada de la computado-
ra. Un procedimiento intuitivo simple consiste en graficar la función sobre una cuadrí-
cula (figura PT6.5) y contar el número de cuadros que se aproximen al área. Este
número multiplicado por el área de cada cuadro proporciona una burda estimación del
área total bajo la curva. Dicha estimación se puede mejorar, a expensas de mayor traba-
jo, usando una cuadrícula más fina.
Otro procedimiento de sentido común es dividir el área en segmentos verticales, o
barras, con una altura igual al valor de la función en el punto medio de cada barra (fi-
gura PT6.6). Después, el área de los rectángulos se calcula y se suma para estimar el
área total. En este procedimiento se supone que el valor en el punto medio de la barra
ofrece una aproximación válida de la altura promedio de la función en cada barra. Como
en el método de la cuadrícula, es posible mejorar las estimaciones al usar más barras (y
en consecuencia más delgadas) para aproximar la integral.
Aunque tales procedimientos tienen utilidad para estimaciones rápidas, existen técni-
cas numéricas alternativas con el mismo propósito. No es de sorprender entonces que los
más simples de estos métodos sean similares, en esencia, a las técnicas sin computadora.
Para la diferenciación, las técnicas numéricas fundamentales utilizan diferencias
divididas finitas para estimar las derivadas. Para datos con error, un procedimiento al-
ternativo consiste en ajustar a los datos una curva suave con una técnica como la de re-
gresión por mínimos cuadrados y luego derivar esta curva para obtener las estimaciones
correspondientes.
De la misma forma, se dispone de integración numérica o de métodos de cuadratura
para obtener integrales. Dichos métodos, que, de hecho, son más fáciles de implementar

6/12/06 13:59:38
Chapra-21.indd 607 6/12/06 13:59:38
Chapra-21.indd 607