Page 633 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT6.1 MOTIVACIÓN 609

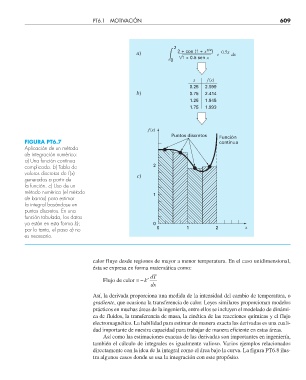
2 2 + cos (1 + x 3/2 )
a) e 0.5x dx
0 1 + 0.5 sen x

x f (x)
0.25 2.599
b) 0.75 2.414
1.25 1.945
1.75 1.993

f (x)
Puntos discretos Función
FIGURA PT6.7 continua
Aplicación de un método
de integración numérico:
a) Una función continua
complicada. b) Tabla de 2
valores discretos de f (x)
generados a partir de c)
la función. c) Uso de un
método numérico (el método 1
de barras) para estimar
la integral basándose en
puntos discretos. En una
función tabulada, los datos
ya están en esta forma b); 0
por lo tanto, el paso a) no 0 1 2 x
es necesario.

calor fluye desde regiones de mayor a menor temperatura. En el caso unidimensional,
ésta se expresa en forma matemática como:
dT
Flujo de calor = – ′ k
dx
Así, la derivada proporciona una medida de la intensidad del cambio de temperatura, o
gradiente, que ocasiona la transferencia de calor. Leyes similares proporcionan modelos
prácticos en muchas áreas de la ingeniería, entre ellos se incluyen el modelado de dinámi-
ca de fluidos, la transferencia de masa, la cinética de las reacciones químicas y el flujo
electromagnético. La habilidad para estimar de manera exacta las derivadas es una cuali-
dad importante de nuestra capacidad para trabajar de manera eficiente en estas áreas.
Así como las estimaciones exactas de las derivadas son importantes en ingeniería,
también el cálculo de integrales es igualmente valioso. Varios ejemplos relacionados
directamente con la idea de la integral como el área bajo la curva. La figura PT6.8 ilus-
tra algunos casos donde se usa la integración con este propósito.

6/12/06 13:59:39
Chapra-21.indd 609 6/12/06 13:59:39
Chapra-21.indd 609