Page 635 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT6.1 MOTIVACIÓN 611

y

Media

0 1 2 3 4 5 6 i
a)

y = f (x)

Media

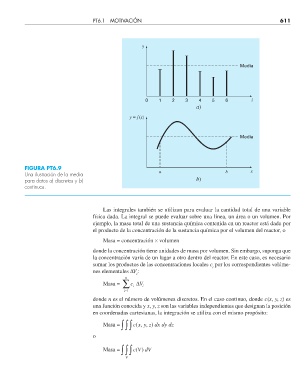
FIGURA PT6.9 x
Una ilustración de la media a b
para datos a) discretos y b) b)
continuos.

Las integrales también se utilizan para evaluar la cantidad total de una variable
física dada. La integral se puede evaluar sobre una línea, un área o un volumen. Por
ejemplo, la masa total de una sustancia química contenida en un reactor está dada por
el producto de la concentración de la sustancia química por el volumen del reactor, o
Masa = concentración × volumen
donde la concentración tiene unidades de masa por volumen. Sin embargo, suponga que
la concentración varía de un lugar a otro dentro del reactor. En este caso, es necesario
sumar los productos de las concentraciones locales c por los correspondientes volúme-
i
nes elementales ∆V :
i
n
∑ c ∆
Masa = i V i
i=1
donde n es el número de volúmenes discretos. En el caso continuo, donde c(x, y, z) es
una función conocida y x, y, z son las variables independientes que designan la posición
en coordenadas cartesianas, la integración se utiliza con el mismo propósito:
∫ ∫ ∫
Masa = c x y z dx dy dz(, , )
o
∫ ∫ ∫
Masa = cV dV()
V

6/12/06 13:59:39
Chapra-21.indd 611 6/12/06 13:59:39
Chapra-21.indd 611