Page 723 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 699

60 200
190
40 175
160
20 135
130
0 122
a) b)

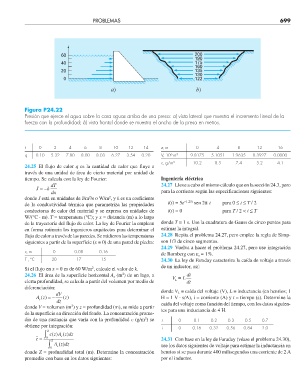
Figura P24.22
Presión que ejerce el agua sobre la cara aguas arriba de una presa: a) vista lateral que muestra el incremento lineal de la
fuerza con la profundidad; b) vista frontal donde se muestra el ancho de la presa en metros.

t 0 2 4 6 8 10 12 14 z, m 0 4 8 12 16
6
q 0.10 5.32 7.80 8.00 8.03 6.27 3.54 0.20 V, 10 m 3 9.8175 5.1051 1.9635 0.3927 0.0000
c, g/m 3 10.2 8.5 7.4 5.2 4.1
24.25 El flujo de calor q es la cantidad de calor que fluye a
través de una unidad de área de cierto material por unidad de
tiempo. Se calcula con la ley de Fourier: Ingeniería eléctrica
dT 24.27 Lleve a cabo el mismo cálculo que en la sección 24.3, pero
J = – k
dx para la corriente según las especificaciones siguientes:
2
2
donde J está en unidades de J/m /s o W/m , y k es un coeficiente
de la conductividad térmica que parametriza las propiedades i(t) = 5e –1.25t sen 2π t para 0 ≤ t ≤ T / 2
conductoras de calor del material y se expresa en unidades de i(t) = 0 para T / 2 < t ≤ T
W/(°C · m). T = temperatura (°C); y x = distancia (m) a lo largo
de la trayectoria del flujo de calor. La ley de Fourier la emplean donde T = 1 s. Use la cuadratura de Gauss de cinco puntos para
en forma rutinaria los ingenieros arquitectos para determinar el estimar la integral.
flujo de calor a través de las paredes. Se midieron las temperaturas 24.28 Repita el problema 24.27, pero emplee la regla de Simp-
siguientes a partir de la superficie (x = 0) de una pared de piedra: son 1/3 de cinco segmentos.
24.29 Vuelva a hacer el problema 24.27, pero use integración
x, m 0 0.08 0.16
de Romberg con e s = 1%.
T , °C 20 17 15 24.30 La ley de Faraday caracteriza la caída de voltaje a través
2
Si el flujo en x = 0 es de 60 W/m , calcule el valor de k. de un inductor, así:
2
24.26 El área de la superficie horizontal A s (m ) de un lago, a V = L di
cierta profundidad, se calcula a partir del volumen por medio de L dt
diferenciación:
donde V L = caída del voltaje (V), L = inductancia (en henrios; 1
Az() = – dV z () H = 1 V · s/A), i = corriente (A) y t = tiempo (s). Determine la
s
dz
3
donde V = volumen (m ) y z = profundidad (m), se mide a partir caída del voltaje como función del tiempo, con los datos siguien-
tes para una inductancia de 4 H.
de la superficie en dirección del fondo. La concentración prome-
3
dio de una sustancia que varía con la profundidad c (g/m ) se t 0 0.1 0.2 0.3 0.5 0.7
obtiene por integración: i 0 0.16 0.32 0.56 0.84 2.0
Z
() ()
cz A z dz
c = ∫ 0 s 24.31 Con base en la ley de Faraday (véase el problema 24.30),
Z
Az dz
()
∫ 0 s use los datos siguientes de voltaje para estimar la inductancia en
donde Z = profundidad total (m). Determine la concentración henrios si se pasa durante 400 milisegundos una corriente de 2 A
promedio con base en los datos siguientes: por el inductor.
6/12/06 14:01:19
Chapra-24.indd 699 6/12/06 14:01:19
Chapra-24.indd 699