Page 841 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

27.3 EDO Y VALORES PROPIOS CON BIBLIOTECAS Y PAQUETES 817

En MATLAB también se incluyen funciones diseñadas para sistemas rígidos,
definidas por ODE15S y ODE23S. Como se muestra en el siguiente ejemplo, éstas fun-
cionan bien cuando fallan las funciones estándar.

EJEMPLO 27.10 MATLAB para EDO rígidas

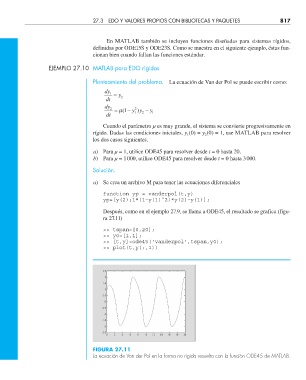
Planteamiento del problema. La ecuación de Van der Pol se puede escribir como:
dy
1 = y
dt 2
dy
2 = µ( 1− yy − y
2
)
dt 1 2 1
Cuando el parámetro µ es muy grande, el sistema se convierte progresivamente en
rígido. Dadas las condiciones iniciales, y (0) = y (0) = 1, use MATLAB para resolver
2
1
los dos casos siguientes.
a) Para µ = 1, utilice ODE45 para resolver desde t = 0 hasta 20.
b) Para µ = 1 000, utilice ODE45 para resolver desde t = 0 hasta 3 000.
Solución.

a) Se crea un archivo M para tener las ecuaciones diferenciales

function yp = vanderpol(t,y)
yp=[y(2);1*(1–y(1)ˆ2)*y(2)–y(1)];

Después, como en el ejemplo 27.9, se llama a ODE45, el resultado se grafica (figu-
ra 27.11)

>> tspan=[0,20];
>> y0=[1,1];
>> [t,y]=ode45(‘vanderpol’,tspan,y0);
>> plot(t,y(:,1))

FIGURA 27.11
La ecuación de Van der Pol en la forma no rígida resuelta con la función ODE45 de MATLAB.

6/12/06 14:03:09
Chapra-27.indd 817 6/12/06 14:03:09
Chapra-27.indd 817