Page 851 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

28.1 USO DE LAS EDO PARA ANALIZAR LA RESPUESTA TRANSITORIA 827

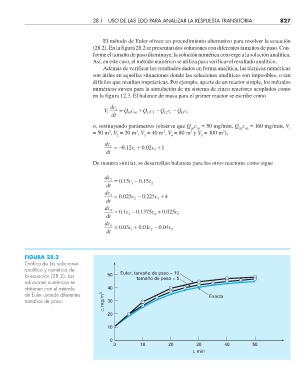
El método de Euler ofrece un procedimiento alternativo para resolver la ecuación
(28.2). En la figura 28.2 se presentan dos soluciones con diferentes tamaños de paso. Con-
forme el tamaño de paso disminuye, la solución numérica converge a la solución analítica.
Así, en este caso, el método numérico se utiliza para verificar el resultado analítico.
Además de verificar los resultados dados en forma analítica, las técnicas numéricas
son útiles en aquellas situaciones donde las soluciones analíticas son imposibles, o tan
difíciles que resultan imprácticas. Por ejemplo, aparte de un reactor simple, los métodos
numéricos sirven para la simulación de un sistema de cinco reactores acoplados como
en la figura 12.3. El balance de masa para el primer reactor se escribe como
dc
V 1 1 = Qc + Q c − Qc − Q c
15 1
12 1
01 01
31 3
dt
o, sustituyendo parámetros (observe que Q c = 50 mg/min, Q c = 160 mg/min, V
01 01 03 03 1
3
3
3
3
3
= 50 m , V = 20 m , V = 40 m , V = 80 m y V = 100 m ),
2 3 4 5
dc
1 =− 0 12. c + 0 02. c + 1
dt 1 3
De manera similar, se desarrollan balances para los otros reactores como sigue
dc
2 = 015. c − 015. c
dt 1 2
dc 3 = 0 025. c − 0 225. c + 4
dt 2 3
dc 4 = 0. c 1 − 0 1375. c + 0 025. c
dt 3 4 5
dc 5 = 003. c + 001. c − 004. c
dt 1 2 5

FIGURA 28.2
Gráfi ca de las soluciones
analítica y numérica de Euler, tamaño de paso = 10
la ecuación (28.2). Las 50 tamaño de paso = 5
soluciones numéricas se
obtienen con el método 40
de Euler usando diferentes Exacta
c, mg/m 3
tamaños de paso. 30
20

10

0
0 10 20 30 40 50
t, min

6/12/06 14:03:36
Chapra-28.indd 827 6/12/06 14:03:36
Chapra-28.indd 827