Page 247 - Matematik Tingkata 3

Bab 9 Garis Lurus

TIP
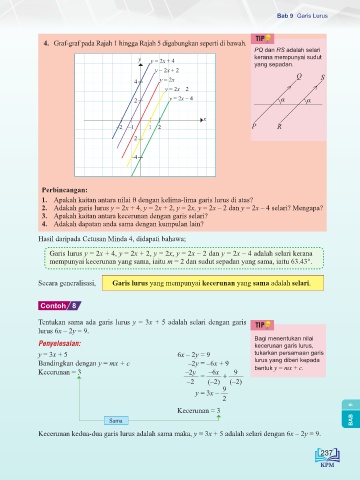
4. Graf-graf pada Rajah 1 hingga Rajah 5 digabungkan seperti di bawah.
PQ dan RS adalah selari
y y = 2x + 4 kerana mempunyai sudut
yang sepadan.
y = 2x + 2
4 y = 2x Q S
y = 2x – 2
2 y = 2x – 4 α α

x
–2 –1 1 2 P R
–2

–4

Perbincangan:
1. Apakah kaitan antara nilai θ dengan kelima-lima garis lurus di atas?
2. Adakah garis lurus y = 2x + 4, y = 2x + 2, y = 2x, y = 2x – 2 dan y = 2x – 4 selari? Mengapa?
3. Apakah kaitan antara kecerunan dengan garis selari?
4. Adakah dapatan anda sama dengan kumpulan lain?

Hasil daripada Cetusan Minda 4, didapati bahawa;
Garis lurus y = 2x + 4, y = 2x + 2, y = 2x, y = 2x – 2 dan y = 2x – 4 adalah selari kerana
mempunyai kecerunan yang sama, iaitu m = 2 dan sudut sepadan yang sama, iaitu 63.43°.

Secara generalisasi, Garis lurus yang mempunyai kecerunan yang sama adalah selari.

Contoh 8

Tentukan sama ada garis lurus y = 3x + 5 adalah selari dengan garis TIP
lurus 6x – 2y = 9.
Bagi menentukan nilai
Penyelesaian: kecerunan garis lurus,
y = 3x + 5 6x – 2y = 9 tukarkan persamaan garis
Bandingkan dengan y = mx + c –2y = –6x + 9 lurus yang diberi kepada
9
Kecerunan = 3 —— = —— + —— bentuk y = mx + c.
–2y –6x
–2 (–2) (–2)

9
y = 3x – —
2 9
Kecerunan = 3
Sama BAB
Saiz sebenar
Kecerunan kedua-dua garis lurus adalah sama maka, y = 3x + 5 adalah selari dengan 6x – 2y = 9.

237