Page 6 - révision bac math

Ann´ ee Scolaire Section : Bac
[ S´erie R´evision N°3 \
2016/2017 Sections Scientifiques

g(x)
e) Calculer lim . Interpr´ eter graphiquement le r´ esultat.
x→+∞ x
f) Tracer C g
3
Z
2 −2x
(II) On pose I = x e dx.
0
1 25
−6
`
1. A l’aide d’une double int´ egration par partie montrer que I = − e .
4 4
2. On d´ efinit le solide S obtenu par r´ evolution autour de l’axe des abscisses de la courbe y = f(x) pour
0 ≤ x ≤ 3.
Exprimer le volume V du solide S en fonction de I. D´ eterminer alors la valeur exacte de V en unit´ e
de volume.

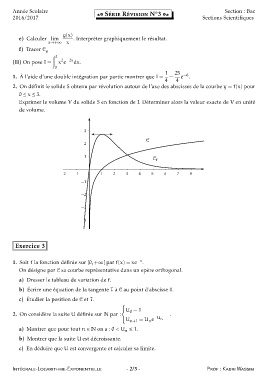
3
b
C
2

1
C f

−2 −1 1 2 3 4 5 6 7 8
−1

−2

−3

−4

Exercice 3

1. Soit f la fonction d´ efinie sur [0,+∞[ par f(x) = xe −x .
On d´ esigne par C sa courbe repr´ esentative dans un ep` ere orthogonal.

a) Dresser le tableau de variation de f.
´
b) Ecrire une ´ equation de la tangente T ` a C au point d’abscisse 0.
´
c) Etudier la position de C et T.

U = 1

0
2. On consid` ere la suite U d´ efinie sur N par : .
 U n+1 = U e −U n
n
a) Montrer que pour tout n ∈ N on a : 0 < U ≤ 1.
n
b) Montrer que la suite U est d´ ecroissante.

c) En d´ eduire que U est convergente et calculer sa limite.

Int´ egrale-Logarithme-Exponentielle - 2/3 - Prof : Kadri Wassim