Page 20 - Fisica_1_BGU

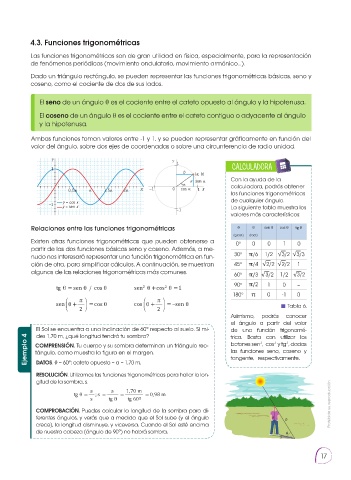
4.3. Funciones trigonométricas

Las funciones trigonométricas son de gran utilidad en física, especialmente, para la representación
de fenómenos periódicos (movimiento ondulatorio, movimiento armónico…).

Dado un triángulo rectángulo, se pueden representar las funciones trigonométricas básicas, seno y
coseno, como el cociente de dos de sus lados.

El seno de un ángulo θ es el cociente entre el cateto opuesto al ángulo y la hipotenusa.

El coseno de un ángulo θ es el cociente entre el cateto contiguo o adyacente al ángulo
y la hipotenusa.

Ambas funciones toman valores entre -1 y 1, y se pueden representar gráficamente en función del
valor del ángulo, sobre dos ejes de coordenadas o sobre una circunferencia de radio unidad.

Y Y
1 CALCULADORA
1
b (a, b)
Con la ayuda de la
a sen α
α calculadora, podrás obtener
0,5π π 1,5π 2π X −1 0 cos α 1 X
las funciones trigonométricas
de cualquier ángulo.
y = cos x
−1 y = sen x La siguiente tabla muestra los
−1
valores más característicos:
Relaciones entre las funciones trigonométricas θ θ sen θ cos θ tg θ
(grad.) (rad.)
Existen otras funciones trigonométricas que pueden obtenerse a 0 o 0 0 1 0
partir de las dos funciones básicas seno y coseno. Además, a me-
nudo nos interesará representar una función trigonométrica en fun- 30 o �/6 1/2 √ 3/2 √ 3/3
ción de otra, para simplificar cálculos. A continuación, se muestran 45 o �/4 √ 2/2 √ 2/2 1
algunas de las relaciones trigonométricas más comunes. 60 o �/3 √ 3/2 1/2 √ 3/2

90 o �/2 1 0 –
2
tg = sen cos sen +cos 2 =1
180 o � 0 -1 0
sen + =cos cos + = sen Tabla 6.
2 2
Asimismo, podrás conocer
el ángulo a partir del valor
El Sol se encuentra a una inclinación de 60° respecto al suelo. Si mi- de una función trigonomé-
des 1,70 m, ¿qué longitud tendrá tu sombra?
trica. Basta con utilizar los
Ejemplo 4 COMPRENSIÓN. Tu cuerpo y su sombra determinan un triángulo rec- botones sen , cos y tg , dadas
-1
-1
-1
las funciones seno, coseno y
tángulo, como muestra la figura en el margen.
tangente, respectivamente.
DATOS. θ = 60°; cateto opuesto = a = 1,70 m.
RESOLUCIÓN. Utilizamos las funciones trigonométricas para hallar la lon-
gitud de la sombra, s.
a a 1,70 m
tg = ;s = = = 0,98 m
s tg tg 60º
COMPROBACIÓN. Puedes calcular la longitud de la sombra para di- Prohibida su reproducción
ferentes ángulos, y verás que a medida que el Sol sube (y el ángulo a h
crece), la longitud disminuye, y viceversa. Cuando el Sol esté encima
de nuestra cabeza (ángulo de 90°) no habrá sombra. θ
s

17