Page 18 - Fisica_1_BGU

3.3. Ecuaciones de segundo grado EN GRUPO Y TAMBIÉN TICS RECORTABLES CALCULADORA
y también:
Las ecuaciones de segundo grado o ecuaciones cuadráticas
con una incógnita son ecuaciones de la forma: La ecuación de la recta
es ax + b = y, que, cuando
2
ax + bx + c = 0 y = 0, no es más que la ecua-
ción de primer grado con una
y sus dos soluciones o raíces se encuentran a partir de la fórmula incógnita; es decir: ax + b = 0.
cuadrática: Así pues, la solución de esta
2
√
- b ± b - 4ac ecuación nos indica el punto
x =
2a de corte de la recta con el eje
3.4. Rectas y parábolas de las abscisas (eje X), ya que
en este punto y = 0.
A menudo, te interesará representar la relación que guardan dos
magnitudes físicas (como la posición y el tiempo o la fuerza y la Del mismo modo, la ecuación
aceleración, por ejemplo). de segundo grado es una pa-
rábola, ax + bx + c = y, con
2
Cuando la relación entre dos magnitudes o variables x e y sea de y = 0. Así pues, las soluciones de
la forma y = mx + n, la representación será una recta, donde m es esta ecuación nos indican los
su pendiente y n es la ordenada en el origen. puntos de corte de la parábo-
la con el eje de las abscisas.
Cuando la relación entre ambas sea de la forma y = ax + bx + c,
2
la representación será una parábola de eje paralelo a alguno de Y
los ejes de coordenadas. Esta es la curva que describe cualquier
objeto cuando se lanza: un proyectil, una piedra, etc. 7 6
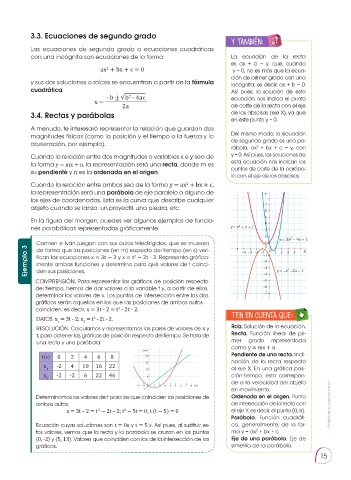
En la figura del margen, puedes ver algunos ejemplos de funcio- 5 4
nes parabólicas representadas gráficamente. y = x + x + 1 3
2
2
y = 3x − 4x + 1
2
Carmen e Iván juegan con sus autos teledirigidos, que se mueven 1 0 0
Ejemplo 3 fican las ecuaciones x = 3t − 2 y x = t − 2t - 2. Representa gráfica- −4 −3 −2 −1 −1 1 2 3 2 4 X
de forma que las posiciones (en m) respecto del tiempo (en s) veri-
2
−2
mente ambas funciones y determina para qué valores de t coinci-
−3
den sus posiciones.
COMPRENSIÓN. Para representar las gráficas de posición respecto −4 y = −x −2x − 1
−5
del tiempo, hemos de dar valores a la variable t y, a partir de ellos, −6
determinar los valores de x. Los puntos de intersección entre las dos −7
gráficas serán aquellos en los que las posiciones de ambos autos
CALCULADORA
coinciden; es decir, x = 3t - 2 = t - 2t - 2. EN GRUPO Y TAMBIÉN: Ten en cuenta que: TEN EN CUENTA QUE:
TIC
2
DATOS. x = 3t - 2; x = t - 2t - 2.
2
1 2
RESOLUCIÓN. Calculamos y representamos los pares de valores de x y Raíz. Solución de la ecuación.
t, para obtener las gráficas de posición respecto del tiempo. Se trata de Recta. Función lineal de pri-
una recta y una parábola: mer grado representada
como y = mx + n.
x (m)
20 Pendiente de una recta. Incli-
t(s) 0 2 4 6 8
15 nación de la recta respecto
x -2 4 10 16 22 al eje X. En una gráfica posi-
1 10
x -2 -2 6 22 46 5 ción-tiempo, esta correspon-
2
de a la velocidad del objeto
–2 –1 0 1 2 3 4 5 6 7 8 t (s)
en movimiento.
Determinamos los valores de t para los que coinciden las posiciones de Ordenada en el origen. Punto
ambos autos: de intersección de la recta con Prohibida su reproducción
2
2
x = 3t – 2 = t − 2t – 2; t − 5t = 0; t (t − 5) = 0 el eje Y; es decir, el punto (0, n).
Parábola. Función cuadráti-
Ecuación cuyas soluciones son t = 0s y t = 5 s. Así pues, al sustituir es- ca, generalmente, de la for-
2
tos valores, vemos que la recta y la parábola se cruzan en los puntos ma y = ax + bx + c.
(0, -2) y (5, 13). Valores que coinciden con los de la intersección de las Eje de una parábola. Eje de
gráficas. simetría de la parábola.
15