Page 144 - 9780077418427.pdf

/Users/user-f465/Desktop
tiL12214_ch05_115-138.indd Page 121 9/1/10 9:39 PM user-f465
tiL12214_ch05_115-138.indd Page 121 9/1/10 9:39 PM user-f465 /Users/user-f465/Desktop

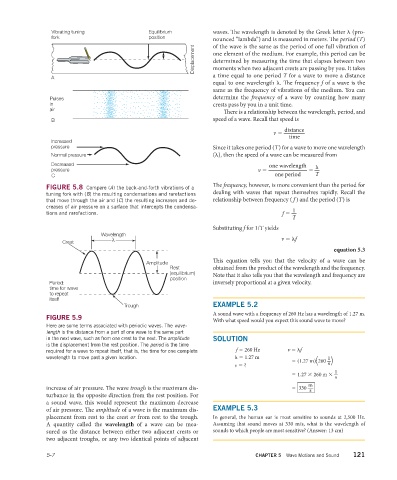
Vibrating tuning Equilibrium waves. The wavelength is denoted by the Greek letter λ (pro-

fork position nounced “lambda”) and is measured in meters. Th e period (T)
of the wave is the same as the period of one full vibration of
Displacement one element of the medium. For example, this period can be
determined by measuring the time that elapses between two
moments when two adjacent crests are passing by you. It takes
A a time equal to one period T for a wave to move a distance
equal to one wavelength λ. Th e frequency f of a wave is the
same as the frequency of vibrations of the medium. You can
Pulses determine the frequency of a wave by counting how many
in crests pass by you in a unit time.
air

There is a relationship between the wavelength, period, and
B speed of a wave. Recall that speed is
_
distance

v =
time
Increased
pressure Since it takes one period (T) for a wave to move one wavelength
Normal pressure (λ), then the speed of a wave can be measured from
Decreased one wavelength λ
=

pressure v = __ _

C one period T
Th e frequency, however, is more convenient than the period for
FIGURE 5.8 Compare (A) the back-and-forth vibrations of a
tuning fork with (B) the resulting condensations and rarefactions dealing with waves that repeat themselves rapidly. Recall the
that move through the air and (C) the resulting increases and de- relationship between frequency ( f ) and the period (T) is
creases of air pressure on a surface that intercepts the condensa- 1 _

tions and rarefactions. f =
T
Substituting f for 1/T yields
Wavelength
Crest λ v = λf
equation 5.3

Amplitude This equation tells you that the velocity of a wave can be
Rest obtained from the product of the wavelength and the frequency.
(equilibrium) Note that it also tells you that the wavelength and frequency are
position
Period: inversely proportional at a given velocity.
time for wave
to repeat
itself
Trough EXAMPLE 5.2
A sound wave with a frequency of 260 Hz has a wavelength of 1.27 m.
FIGURE 5.9
With what speed would you expect this sound wave to move?
Here are some terms associated with periodic waves. The wave-
length is the distance from a part of one wave to the same part
in the next wave, such as from one crest to the next. The amplitude SOLUTION
is the displacement from the rest position. The period is the time
required for a wave to repeat itself, that is, the time for one complete f = 260 Hz v = λf
wavelength to move past a given location. λ = 1.27 m 1 _
= (1.27 m) (260 )
v = ? s
1 _
= 1.27 × 260 m ×

s
m _

increase of air pressure. Th e wave trough is the maximum dis- = 330
s
turbance in the opposite direction from the rest position. For
a sound wave, this would represent the maximum decrease
of air pressure. Th e amplitude of a wave is the maximum dis- EXAMPLE 5.3
placement from rest to the crest or from rest to the trough. In general, the human ear is most sensitive to sounds at 2,500 Hz.
A quantity called the wavelength of a wave can be mea- Assuming that sound moves at 330 m/s, what is the wavelength of
sured as the distance between either two adjacent crests or sounds to which people are most sensitive? (Answer: 13 cm)
two adjacent troughs, or any two identical points of adjacent
5-7 CHAPTER 5 Wave Motions and Sound 121