Page 20 - MODULE & MORE ADDMATHS TG4

Matematik Tambahan Tingkatan 4 Bonus untuk Guru

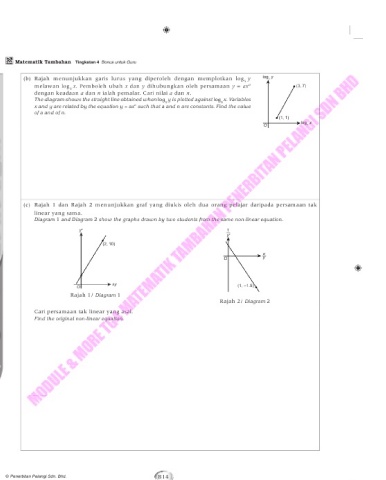
(b) Rajah menunjukkan garis lurus yang diperoleh dengan memplotkan log y log y
5
5
melawan log x. Pemboleh ubah x dan y dihubungkan oleh persamaan y = ax (3, 7)
n
5
dengan keadaan a dan n ialah pemalar. Cari nilai a dan n.
The diagram shows the straight line obtained when log y is plotted against log x. Variables
5
5
x and y are related by the equation y = ax such that a and n are constants. Find the value
n
of a and of n.
(1, 1)
5
O log x
y = ax
n
c = log a

L log y = n log x + log a = –2 5
5
5
5
a = 5
E kecerunan = n = 7 – 1 = 1 –2
3 – 1
= 3
25
M Y = 3X + c melalui (1, 1) \ a = 25 dan n = 3
1
B 1 = 3(1) + c
c = –2
A (c) Rajah 1 dan Rajah 2 menunjukkan graf yang diukis oleh dua orang pelajar daripada persamaan tak
R linear yang sama.
Diagram 1 and Diagram 2 show the graphs drawn by two students from the same non-linear equation.
A y 2 1 y 2
N (2, 10)
O x y

xy (1, –1.5)
O
P Rajah 1/ Diagram 1
Rajah 2/ Diagram 2
B Cari persamaan tak linear yang asal.
Find the original non-linear equation.
D Rajah 1: y = m(xy) + c …… 1 4 × 2: 10 = 2m + c
2 = 2m – 3c
2
Gantikan (2, 10) ke dalam 1:
2:
10 = m(2) + c …… 2 Tolak: –8 = –4c
c = 2
14 1 ÷ y : y 2 2 = m (xy) + y c 2 Ganti c = 2 ke dalam 2:
2
y
2
y
1
x
1 = m 1 2 1 2 …… 3 10 = 2m + 2
+ c
m = 4
y
y
2
2
Gantikan (1, –1.5) ke dalam 3: Persamaan tak linear yang asal ialah y = 4xy + 2.
1 = m(1) + c(–1.5) …… 4
Selesaikan persamaan serentak 2 dan 4:
10 = 2m + c …… 2
1 = m – 1.5c …… 4

© Penerbitan Pelangi Sdn. Bhd. B14

Bonus utk Guru.indd 14 12/11/2019 12:01 PM