Page 19 - PBD Plus Matematik T5 (EG)

Matematik Tingkatan 5 Bab 1 Ubahan
SP 1.2.2 Menentukan hubungan antara dua pemboleh ubah bagi suatu ubahan songsang.

16. Selesaikan. TP 2
Solve.
Contoh
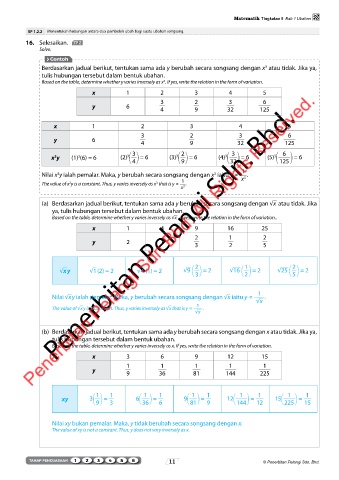
Berdasarkan jadual berikut, tentukan sama ada y berubah secara songsang dengan x atau tidak. Jika ya,
3
tulis hubungan tersebut dalam bentuk ubahan.
Based on the table, determine whether y varies inversely as x . If yes, write the relation in the form of variation.
3
x 1 2 3 4 5

3 2 3 6
Penerbitan Pelangi Sdn. Bhd.
y 6
4 9 32 125
x 1 2 3 4 5
3 2 3 6
y 6 4 9 32 125

2
6
3
3
x y (1) (6) = 6 (2) 3 1 2 = 6 (3) 3 1 2 = 6 (4) 3 1 2 = 6 (5) 3 1 125 2 = 6
3
3
4
32
9
1
3
Nilai x y ialah pemalar. Maka, y berubah secara songsang dengan x iaitu y ∝ x 3 .
3
The value of x y is a constant. Thus, y varies inversely as x that is y ∝ 1 .
3
3
x 3
(a) Berdasarkan jadual berikut, tentukan sama ada y berubah secara songsang dengan √x atau tidak. Jika
ya, tulis hubungan tersebut dalam bentuk ubahan.
Based on the table, determine whether y varies inversely as √x . If yes, write the relation in the form of variation..
x 1 4 9 16 25
2 1 2
y 2 1 3 2 5
2
2
1
√x y √1 (2) = 2 √4 (1) = 2 √9 1 2 = 2 √16 1 2 = 2 √25 1 2 = 2
3
5
2
1
Nilai √x y ialah pemalar. Maka, y berubah secara songsang dengan √x iaitu y ∝ √x .
1
The value of √x y is a constant. Thus, y varies inversely as √x that is y ∝ .
√x

(b) Berdasarkan jadual berikut, tentukan sama ada y berubah secara songsang dengan x atau tidak. Jika ya,
tulis hubungan tersebut dalam bentuk ubahan.
Based on the table, determine whether y varies inversely as x. If yes, write the relation in the form of variation.
x 3 6 9 12 15
1 1 1 1 1
y 9 36 81 144 225

1
1
1
1
1
1
1
xy 3 1 2 = 1 6 1 2 = 1 9 1 2 = 1 12 1 144 2 = 12 15 1 225 2 = 15
36
3
9
9
81
6
Nilai xy bukan pemalar. Maka, y tidak berubah secara songsang dengan x.
The value of xy is not a constant. Thus, y does not vary inversely as x.
Tahap penguasaan 1 2 3 4 5 6 11 © Penerbitan Pelangi Sdn. Bhd.