Page 720 - LIBRO DE ACTAS-II-JORINVEDUC-2016

Objetivo: Se observó la dificultad, de los alumnos al trabajar con funciones inversas, en cuanto
a cómo relacionarlas, es decir la función directa con su inversa: a) obtener una a partir de la otra y b)
la simetría con respecto a la función identidad de ambas funciones.
Fundamento teórico: Dada una función, si la misma es uno a uno, es decir si f(x1) ≠ f(x2)
entonces siempre que x1 y x2 pertenezcan al dominio de f se tendrá que x1≠ x2, tendremos que dicha
función tiene función inversa.

Instrucciones para interactuar con el applet: En la Fig.1 se grafica la función exponencial (g)
y su inversa, la función logaritmo (h). Se disponede tres deslizadores mediante los cuales puede
seleccionarse la base del logaritmo, el desplazamiento horizontal y vertical y las formulas
correspondientes se indican junto a cada función. Al ir desplazando los deslizadores cambia la
función, como así también la inversa, lo que permite que el alumno pueda comprobar que en todos
los casos ambas funciones son simétricas a la función identidad, representada por la recta y = x.

2.- Derivada de la función en un punto.
Objetivo: El propósito de esta aplicación es que el alumno visualice la interpretación
geométrica de la derivada.

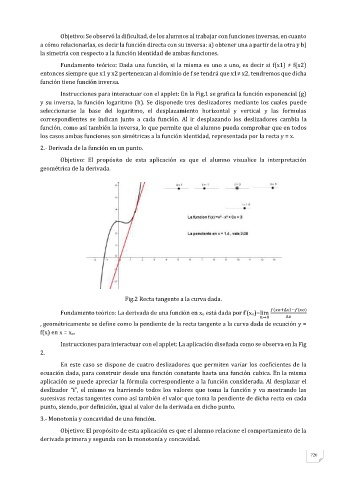
Fig.2 Recta tangente a la curva dada.
( +∆ )− ( )
Fundamento teórico: La derivada de una función en xo está dada por f’(xo)=lim
→0 ∆
, geométricamente se define como la pendiente de la recta tangente a la curva dada de ecuación y =
f(x) en x = xo.

Instrucciones para interactuar con el applet: La aplicación diseñada como se observa en la Fig
2.

En este caso se dispone de cuatro deslizadores que permiten variar los coeficientes de la
ecuación dada, para construir desde una función constante hasta una función cubica. En la misma
aplicación se puede apreciar la fórmula correspondiente a la función considerada. Al desplazar el
deslizador “i”, el mismo va barriendo todos los valores que toma la función y va mostrando las
sucesivas rectas tangentes como así también el valor que toma la pendiente de dicha recta en cada
punto, siendo, por definición, igual al valor de la derivada en dicho punto.

3.- Monotonía y concavidad de una función.

Objetivo: El propósito de esta aplicación es que el alumno relacione el comportamiento de la
derivada primera y segunda con la monotonía y concavidad.

720