Page 721 - LIBRO DE ACTAS-II-JORINVEDUC-2016

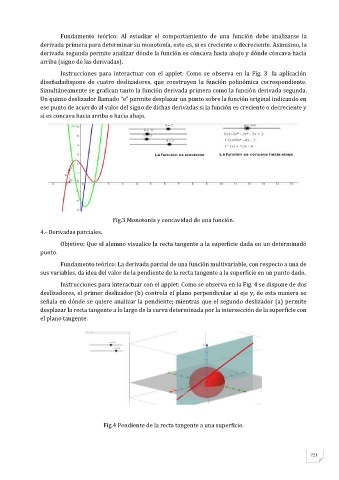
Fundamento teórico: Al estudiar el comportamiento de una función debe analizarse la
derivada primera para determinar su monotonía, esto es, si es creciente o decreciente. Asimismo, la
derivada segunda permite analizar dónde la función es cóncava hacia abajo y dónde cóncava hacia
arriba (signo de las derivadas).
Instrucciones para interactuar con el applet: Como se observa en la Fig. 3 la aplicación
diseñadadispone de cuatro deslizadores, que construyen la función polinómica correspondiente.
Simultáneamente se grafican tanto la función derivada primera como la función derivada segunda.
Un quinto deslizador llamado “e” permite desplazar un punto sobre la función original indicando en
ese punto de acuerdo al valor del signo de dichas derivadas si la función es creciente o decreciente y
si es cóncava hacia arriba o hacia abajo.

Fig.3 Monotonía y concavidad de una función.

4.- Derivadas parciales.

Objetivo: Que el alumno visualice la recta tangente a la superficie dada en un determinado
punto.

Fundamento teórico: La derivada parcial de una función multivariable, con respecto a una de
sus variables, da idea del valor de la pendiente de la recta tangente a la superficie en un punto dado.

Instrucciones para interactuar con el applet: Como se observa en la Fig. 4 se dispone de dos
deslizadores, el primer deslizador (b) controla el plano perpendicular al eje y, de esta manera se
señala en dónde se quiere analizar la pendiente; mientras que el segundo deslizador (a) permite
desplazar la recta tangente a lo largo de la curva determinada por la intersección de la superficie con
el plano tangente.

Fig.4 Pendiente de la recta tangente a una superficie.

721