Page 159 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

5.3 MÉTODO DE LA FALSA POSICIÓN 135

10
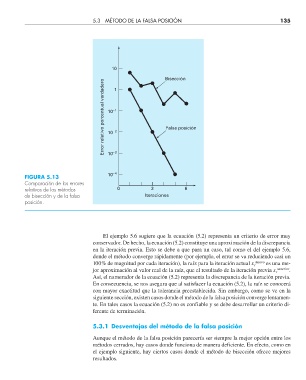
Bisección
Error relativo porcentual verdadero 10 –1 Falsa posición
1

–2
10

–4
10
FIGURA 5.13 10 –3
Comparación de los errores
relativos de los métodos 0 3 6
de bisección y de la falsa Iteraciones
posición.

El ejemplo 5.6 sugiere que la ecuación (5.2) representa un criterio de error muy
conservador. De hecho, la ecuación (5.2) constituye una aproximación de la discrepancia
en la iteración previa. Esto se debe a que para un caso, tal como el del ejemplo 5.6,
donde el método converge rápidamente (por ejemplo, el error se va reduciendo casi un
100% de magnitud por cada iteración), la raíz para la iteración actual x r nuevo es una me-
jor aproximación al valor real de la raíz, que el resultado de la iteración previa x r anterior .
Así, el numerador de la ecuación (5.2) representa la discrepancia de la iteración previa.
En consecuencia, se nos asegura que al satisfacer la ecuación (5.2), la raíz se conocerá
con mayor exactitud que la tolerancia preestablecida. Sin embargo, como se ve en la
siguiente sección, existen casos donde el método de la falsa posición converge lentamen-
te. En tales casos la ecuación (5.2) no es confiable y se debe desarrollar un criterio di-
ferente de terminación.

5.3.1 Desventajas del método de la falsa posición

Aunque el método de la falsa posición parecería ser siempre la mejor opción entre los
métodos cerrados, hay casos donde funciona de manera deficiente. En efecto, como en
el ejemplo siguiente, hay ciertos casos donde el método de bisección ofrece mejores
resultados.

6/12/06 13:49:23
Chapra-05.indd 135 6/12/06 13:49:23
Chapra-05.indd 135