Page 157 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

5.3 MÉTODO DE LA FALSA POSICIÓN 133

f(x)

f(x )
u

x
r
x l
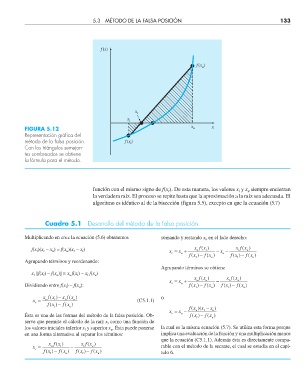
FIGURA 5.12 x u x
Representación gráfi ca del
método de la falsa posición. f(x ) l
Con los triángulos semejan-
tes sombreados se obtiene
la fórmula para el método.

función con el mismo signo de f(x ). De esta manera, los valores x y x siempre encierran
l
u
r
la verdadera raíz. El proceso se repite hasta que la aproximación a la raíz sea adecuada. El
algoritmo es idéntico al de la bisección (figura 5.5), excepto en que la ecuación (5.7)
Cuadro 5.1 Desarrollo del método de la falsa posición

Multiplicando en cruz la ecuación (5.6) obtenemos sumando y restando x u en el lado derecho:

f(x l )(x r – x u ) = f(x u )(x r – x l ) x = x + xf x() − x − xf x()
u
u
l
l
fx − fx( ) fx − fx( )
r u u
()
()
l u l u
Agrupando términos y reordenando:
Agrupando términos se obtiene
x r [f(x l ) – f(x u )] = x u f(x l ) – x l f(x u )
x = x + xf x () − xf x ()
u
u
l
u
Dividiendo entre f(x l ) – f(x u ): r u fx −() fx ( ) fx −() fx ( )
l u l u
x = xf x −() x f x( ) (C5.1.1) o
u
l
l
u
r
fx −() fx( ) x −
l
u
x = x − fx()( l x )
u
u
Ésta es una de las formas del método de la falsa posición. Ob- r u fx −() fx( )
l
u
serve que permite el cálculo de la raíz x r como una función de
los valores iniciales inferior x l y superior x u . Ésta puede ponerse la cual es la misma ecuación (5.7). Se utiliza esta forma porque
en una forma alternativa al separar los términos: implica una evaluación de la función y una multiplicación menos
que la ecuación (C5.1.1). Además ésta es directamente compa-
x = xf x () − xf x () rable con el método de la secante, el cual se estudia en el capí-
l
u
u
l
r
fx −() fx ( ) fx −() fx ( )
l u l u tulo 6.
6/12/06 13:49:22
Chapra-05.indd 133 6/12/06 13:49:22
Chapra-05.indd 133