Page 36 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

12 MODELOS MATEMÁTICOS Y SOLUCIÓN DE PROBLEMAS EN INGENIERÍA

Definición
del problema

Modelo
TEORÍA DATOS
matemático
Herramientas para resolver
problemas: computadoras,
estadística, métodos numéricos,
gráficas, etcétera.

Resultados
numéricos
o gráficos

Relaciones grupales:
programación, optimización,
comunicación, interacción
pública, etcétera.

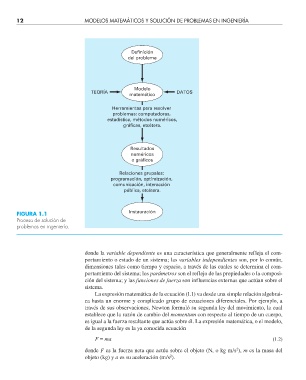
FIGURA 1.1 Instauración
Proceso de solución de
problemas en ingeniería.

donde la variable dependiente es una característica que generalmente refleja el com-
portamiento o estado de un sistema; las variables independientes son, por lo común,
dimensiones tales como tiempo y espacio, a través de las cuales se determina el com-
portamiento del sistema; los parámetros son el reflejo de las propiedades o la composi-
ción del sistema; y las funciones de fuerza son influencias externas que actúan sobre el
sistema.
La expresión matemática de la ecuación (1.1) va desde una simple relación algebrai-
ca hasta un enorme y complicado grupo de ecuaciones diferenciales. Por ejemplo, a
través de sus observaciones, Newton formuló su segunda ley del movimiento, la cual
establece que la razón de cambio del momentum con respecto al tiempo de un cuerpo,
es igual a la fuerza resultante que actúa sobre él. La expresión matemática, o el modelo,
de la segunda ley es la ya conocida ecuación

F = ma (1.2)
2
donde F es la fuerza neta que actúa sobre el objeto (N, o kg m/s ), m es la masa del
2
objeto (kg) y a es su aceleración (m/s ).

6/12/06 13:41:08
Chapra-01.indd 12
Chapra-01.indd 12 6/12/06 13:41:08