Page 361 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

12.4 SISTEMAS MASA-RESORTE 337

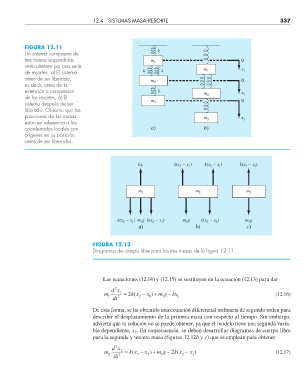
FIGURA 12.11
Un sistema compuesto de k
tres masas suspendidas m 1 0
verticalmente por una serie m x
de resortes. a) El sistema k k 1 1
antes de ser liberado, m 0
es decir, antes de la 2
extensión o compresión k m x
de los resortes. b) El m 2 2
sistema después de ser 3 0
liberado. Observe que las
posiciones de las masas m x
están en referencia a las 3 3
coordenadas locales con a) b)
orígenes en su posición
antes de ser liberadas.

kx 1 k(x – x ) k(x – x ) k(x – x )
2
1
1
3
2
2
m 1 m 2 m 3

k(x – x ) m g k(x – x ) m g k(x – x ) m g
1
3
1
2
2
2
3
2
1
a) b) c)
FIGURA 12.12
Diagramas de cuerpo libre para las tres masas de la fi gura 12.11.
Las ecuaciones (12.14) y (12.15) se sustituyen en la ecuación (12.13) para dar
2
dx
m 1 1 = 2 kx( 2 – x +) m g kx– 1 (12.16)
1
1
dt 2
De esta forma, se ha obtenido una ecuación diferencial ordinaria de segundo orden para
describir el desplazamiento de la primera masa con respecto al tiempo. Sin embargo,
advierta que la solución no se puede obtener, ya que el modelo tiene una segunda varia-
ble dependiente, x . En consecuencia, se deben desarrollar diagramas de cuerpo libre
2
para la segunda y tercera masa (figuras 12.12b y c) que se emplean para obtener
2
dx
m 2 = kx( – x +) m g 2– kx( – x ) (12.17)
2 2 3 2 2 2 1
dt

6/12/06 13:54:36
Chapra-12.indd 337 6/12/06 13:54:36
Chapra-12.indd 337