Page 383 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT4.2 ANTECEDENTES MATEMÁTICOS 359

Determine x, que minimiza o maximiza f(x)
sujeto a
d (x) ≤ a i = 1, 2,..., m (PT4.20)
i
i
e (x) = b i = 1, 2,..., p (PT4.21)
i
i
donde x es un vector de diseño n-dimensional; f(x) es la función objetivo; d (x) son las
i
restricciones de desigualdad; e (x) son las restricciones de igualdad, y a y b son cons-
i
i
i
tantes.
Los problemas de optimización se clasifican considerando la forma de f(x):
• Si f(x) y las restricciones son lineales, tenemos un problema de programación li-
neal.
• Si f(x) es cuadrática y las restricciones son lineales, tenemos un problema de pro-
gramación cuadrática.
• Si f(x) no es lineal ni cuadrática y/o las restricciones no son lineales, tenemos un
problema de programación no lineal.

Se dice también que, cuando las ecuaciones (PT4.20) y (PT4.21) se incluyen, se tiene un
problema de optimización restringido; de otra forma, se trata de un problema de opti-
mización no restringido.
Observe que en problemas restringidos, los grados de libertad están dados por n-p-
m. Generalmente, para obtener una solución, p + m debe ser ≤ n. Si p + m > n, se dice
que el problema está sobrerrestringido.

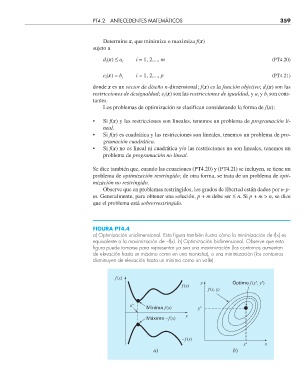
FIGURA PT4.4
a) Optimización unidimensional. Esta fi gura también ilustra cómo la minimización de f(x) es
equivalente a la maximización de –f(x). b) Optimización bidimensional. Observe que esta
fi gura puede tomarse para representar ya sea una maximización (los contornos aumentan
de elevación hasta un máximo como en una montaña), o una minimización (los contornos
disminuyen de elevación hasta un mínimo como un valle).

f (x)
y Óptimo f (x , y )
*
*
f (x)
f (x, y)
x *
Mínimo f (x) y *
x
Máximo – f (x)

– f (x)
x * x
a) b)

6/12/06 13:55:05
Chapra-13.indd 359 6/12/06 13:55:05
Chapra-13.indd 359