Page 42 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

18 MODELOS MATEMÁTICOS Y SOLUCIÓN DE PROBLEMAS EN INGENIERÍA

t, s v, m/s
0 0.00
2 19.60
4 32.00
6 39.85
8 44.82
10 47.97
12 49.96
• 53.39

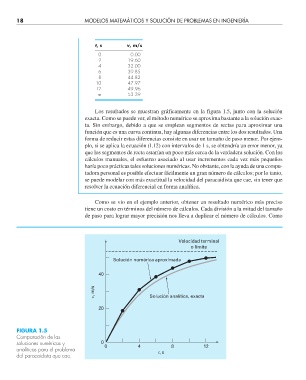
Los resultados se muestran gráficamente en la figura 1.5, junto con la solución
exacta. Como se puede ver, el método numérico se aproxima bastante a la solución exac-
ta. Sin embargo, debido a que se emplean segmentos de rectas para aproximar una
función que es una curva continua, hay algunas diferencias entre los dos resultados. Una
forma de reducir estas diferencias consiste en usar un tamaño de paso menor. Por ejem-
plo, si se aplica la ecuación (1.12) con intervalos de 1 s, se obtendría un error menor, ya
que los segmentos de recta estarían un poco más cerca de la verdadera solución. Con los
cálculos manuales, el esfuerzo asociado al usar incrementos cada vez más pequeños
haría poco prácticas tales soluciones numéricas. No obstante, con la ayuda de una compu-
tadora personal es posible efectuar fácilmente un gran número de cálculos; por lo tanto,
se puede modelar con más exactitud la velocidad del paracaidista que cae, sin tener que
resolver la ecuación diferencial en forma analítica.

Como se vio en el ejemplo anterior, obtener un resultado numérico más preciso
tiene un costo en términos del número de cálculos. Cada división a la mitad del tamaño
de paso para lograr mayor precisión nos lleva a duplicar el número de cálculos. Como

Velocidad terminal
o límite

Solución numérica aproximada

40

v, m/s Solución analítica, exacta

20

FIGURA 1.5
Comparación de las
soluciones numéricas y 0 0 4 8 12
analíticas para el problema
t, s
del paracaidista que cae.

6/12/06 13:41:09
Chapra-01.indd 18
Chapra-01.indd 18 6/12/06 13:41:09