Page 565 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

19.1 AJUSTE DE CURVAS CON FUNCIONES SINUSOIDALES 541

ción muy clara para elegir entre estas funciones y, en cualquier caso, los resultados serán
idénticos. En este capítulo se usará el coseno, que generalmente se expresa como
+ C cos(w t + q) (19.2)
f(t) = A 0 1 0
Así, cuatro parámetros sirven para caracterizar la sinusoide (figura 19.3). El valor medio
A , establece la altura promedio sobre las abscisas. La amplitud C especifica la altura
1
0
de la oscilación. La frecuencia angular w caracteriza con qué frecuencia se presentan
0
los ciclos. Finalmente, el ángulo de fase, o corrimiento de fase q, parametriza en qué
extensión la sinusoide está corrida horizontalmente. Esto puede medirse como la distan-
cia en radianes desde t = 0 hasta el punto donde la función coseno empieza un nuevo
ciclo. Como se ilustra en la figura 19.4a, un valor negativo se conoce como un ángulo

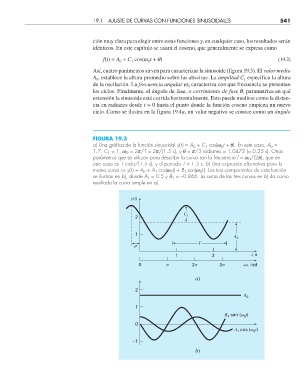
FIGURA 19.3
a) Una gráfi ca de la función sinusoidal y(t ) = A 0 + C 1 cos(w 0 t + q). En este caso, A 0 =
1.7, C 1 = 1, w 0 = 2p/T = 2p/(1.5 s), y q = p/3 radianes = 1.0472 (= 0.25 s). Otros
parámetros que se utilizan para describir la curva son la frecuencia f = w 0 /(2p), que en
este caso es 1 ciclo/(1.5 s), y el periodo T = 1.5 s. b) Una expresión alternativa para la
misma curva es y(t ) = A 0 + A 1 cos(w 0 t) + B 1 sen(w 0 t ). Los tres componentes de esta función
se ilustran en b), donde A 1 = 0.5 y B 1 = –0.866. La suma de las tres curvas en b) da como
resultado la curva simple en a).

y(t)

C
2 1

1
A 0
T

1 2 t, s
0 2 3 t, rad

a)

2
A 0
1
B sen ( t)
1 0
0
A cos ( t)
1
0
–1
b)

6/12/06 13:58:20
Chapra-19.indd 541
Chapra-19.indd 541 6/12/06 13:58:20