Page 612 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

588 ESTUDIO DE CASOS: AJUSTE DE CURVAS

Con el uso de los datos siguientes, determine los parámetros que
Temperatura T, °C minimizan la suma de los cuadrados de los residuos. Asimismo,
2
0 20 40 60 calcule r .
0
[F], nM 0.1 0.5 1 5 10 20 50
[B], nM 10.57 36.61 52.93 82.65 89.46 94.35 101.00
1 Termoclina 20.12 Se tomaron los datos siguientes del tanque de un reactor
Profundidad z, m 2 de agitación para la reacción A → B. Use los datos para hacer
las estimaciones mejores posibles para k 01 y E 1 , para el modelo
cinético siguiente,
E 1
dA
−
3
01
dt = ke − RT A
donde R es la constante de los gases y es igual a 0.00198 Kcal/
mol/K
–dA/dt (moles/L/s) 400 960 2 485 1 600 1 245
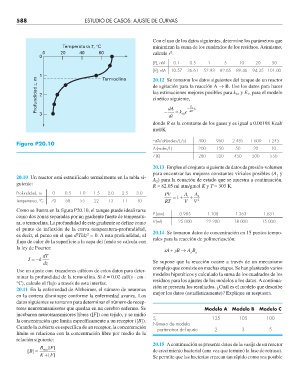
Figura P20.10
A (moles/L) 200 150 50 20 10
T (K) 280 320 450 500 550
20.13 Emplee el conjunto siguiente de datos de presión-volumen
para encontrar las mejores constantes viriales posibles (A 1 y
20.10 Un reactor está estratificado termalmente en la tabla si- A 2 ) para la ecuación de estado que se muestra a continuación.
guiente:
R = 82.05 ml atm/gmol K y T = 303 K.
Profundidad, m 0 0.5 1.0 1.5 2.0 2.5 3.0 PV A A
=+1 1 + 2
Tempertarua, °C 70 68 55 22 13 11 10 RT V V 2
Como se ilustra en la figura P20.10, el tanque puede idealizarse
P (atm) 0.985 1.108 1.363 1.631
como dos zonas separadas por un gradiente fuerte de temperatu-
ra, o termoclina. La profundidad de este gradiente se define como V (ml) 25 000 22 200 18 000 15 000
el punto de inflexión de la curva temperatura-profundidad,
2
2
es decir, el punto en el que d T/dz = 0. A esta profundidad, el 20.14 Se tomaron datos de concentración en 15 puntos tempo-
rales para la reacción de polimerización:
flujo de calor de la superficie a la capa del fondo se calcula con
la ley de Fourier:
xA yB+ → A B y
x
J =− k dT
dz Se supone que la reacción ocurre a través de un mecanismo
complejo que consiste en muchas etapas. Se han planteado varios
Use un ajuste con trazadores cúbicos de estos datos para deter-
modelos hipotéticos y calculado la suma de los cuadrados de los
minar la profundidad de la termoclina. Si k = 0.02 cal/(s · cm ·
residuos para los ajustes de los modelos a los datos. A continua-
°C), calcule el flujo a través de esta interfaz.
ción se presenta los resultados. ¿Cuál es el modelo que describe
20.11 En la enfermedad de Alzheimer, el número de neuronas
mejor los datos (estadísticamente)? Explique su respuesta.
en la corteza disminuye conforme la enfermedad avanza. Los
datos siguientes se tomaron para determinar el número de recep-
tores neurotransmisores que quedan en un cerebro enfermo. Se Modelo A Modelo B Modelo C
incubaron neurotransmisores libres ([F]) con tejido, y se midió
la concentración que limita específicamente a un receptor ([B]). S r 135 105 100
Número de modelo
Cuando la cubierta es específica de un receptor, la concentración
parámetros del ajuste 2 3 5
límite se relaciona con la concentración libre por medio de la
relación siguiente:
20.15 A continuación se presenta datos de la vasija de un reactor
F
[] B = B máx [] de crecimiento bacterial (una vez que terminó la fase de retraso).
K + []
F
Se permite que las bacterias crezcan tan rápido como sea posible
6/12/06 13:59:00
Chapra-20.indd 588 6/12/06 13:59:00
Chapra-20.indd 588