Page 717 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PROBLEMAS 693

10
[ (x)]

F(x) cos

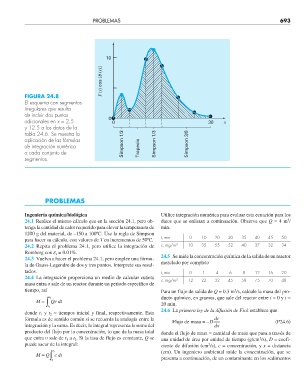
FIGURA 24.8
El esquema con segmentos
irregulares que resulta
de incluir dos puntos
adicionales en x = 2.5 0 0 30 x
y 12.5 a los datos de la
tabla 24.6. Se muestra la
aplicación de las fórmulas
de integración numérica Simpson 1/3 Trapecio Simpson 1/3 Simpson 3/8
a cada conjunto de
segmentos.

PROBLEMAS

Ingeniería química/biológica Utilice integración numérica para evaluar esta ecuación para los
3
24.1 Realice el mismo cálculo que en la sección 24.1, pero ob- datos que se enlistan a continuación. Observe que Q = 4 m /
tenga la cantidad de calor requerido para elevar la temperatura de min.
1200 g del material, de –150 a 100ºC. Use la regla de Simpson
t, min 0 10 20 30 35 40 45 50
para hacer su cálculo, con valores de T en incrementos de 50ºC.
24.2 Repita el problema 24.1, pero utilice la integración de c, mg/m 3 10 35 55 52 40 37 32 34
Romberg con e s = 0.01%.
24.5 Se mide la concentración química de la salida de un reactor
24.3 Vuelva a hacer el problema 24.1, pero emplee una fórmu-
mezclado por completo
la de Gauss-Legendre de dos y tres puntos. Interprete sus resul-
tados. t, min 0 1 4 6 8 12 16 20
24.4 La integración proporciona un medio de calcular cuánta
c, mg/m 3 12 22 32 45 58 75 70 48
masa entra o sale de un reactor durante un periodo específico de
tiempo, así Para un flujo de salida de Q = 0.3 m /s, calcule la masa del pro-
3
M = ∫ t 2 Qc dt ducto químico, en gramos, que sale del reactor entre t = 0 y t =
t 1 20 min.
24.6 La primera ley de la difusión de Fick establece que
donde t 1 y t 2 = tiempos inicial y final, respectivamente. Esta
fórmula es de sentido común si se recuerda la analogía entre la dc
Flujo de masa = –D (P24.6)
integración y la suma. Es decir, la integral representa la suma del dx
producto del flujo por la concentración, lo que da la masa total donde el flujo de masa = cantidad de masa que pasa a través de
que entra o sale de t 1 a t 2 . Si la tasa de flujo es constante, Q se una unidad de área por unidad de tiempo (g/cm /s), D = coefi-
2
puede sacar de la integral: ciente de difusión (cm /s), c = concentración, y x = distancia
2
∫
t 2
M = Q c dt (cm). Un ingeniero ambiental mide la concentración, que se
t 1 presenta a continuación, de un contaminante en los sedimentos

Chapra-24.indd 693 6/12/06 14:01:16
6/12/06 14:01:16
Chapra-24.indd 693