Page 714 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

690 ESTUDIO DE CASOS

durante el proceso del cálculo. En tales casos, la ecuación para el trabajo ahora se ex-
presa como
W = ∫ x n F x dx() (24.14)
x 0
donde W = trabajo (lb · ft), x y x = las posiciones inicial y final, respectivamente, y
n
0
F(x) es una fuerza que varía con la posición. Si F(x) es fácil de integrar, la ecuación
(24.14) se puede resolver en forma analítica. No obstante, en la solución de un problema
real, quizá la fuerza no se exprese de esa manera. De hecho, cuando se analizan los
datos obtenidos de mediciones, la fuerza podría estar disponible sólo en forma tabular.
En tales casos, la integración numérica es la única opción viable para la evaluación.
Se obtiene mayor complejidad si el ángulo entre la fuerza y la dirección del movi-
miento también varía en función de la posición (figura 24.5). La ecuación del trabajo
llega a dificultarse aún más al tomar en cuenta este efecto, entonces
W = ∫ x n F x( ) cos[ (θ x dx)] (24.15)
x 0
De nuevo, si F(x) y q(x) son funciones sencillas, la ecuación (24.15) se podría resolver
de manera analítica. Sin embargo, como se representa en la figura 24.5, es más común
que la relación funcional sea complicada. En tal situación, los métodos numéricos ofre-
cen la única alternativa para determinar la integral.

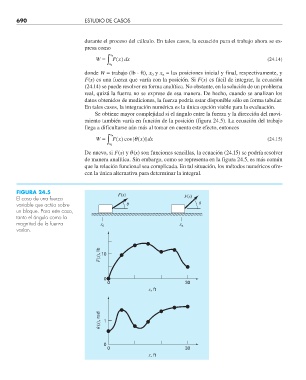
FIGURA 24.5 F(x)
El caso de una fuerza F(x)
variable que actúa sobre
un bloque. Para este caso,
tanto el ángulo como la
magnitud de la fuerza x x
0 n
varían.

F(x), lb 10

0
0 30
x, ft

(x), rad 1

0
0 30
x, ft

6/12/06 14:01:15
Chapra-24.indd 690 6/12/06 14:01:15
Chapra-24.indd 690