Page 716 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

692 ESTUDIO DE CASOS

[ (x)]
F (x) cos

Trabajo

0 30
x, ft
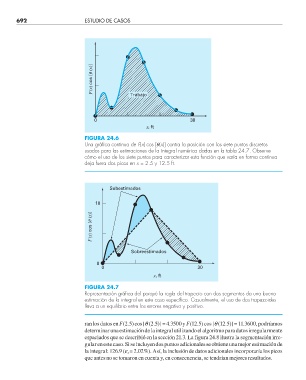
FIGURA 24.6
Una gráfi ca continua de F(x) cos [q(x)] contra la posición con los siete puntos discretos
usados para las estimaciones de la integral numérica dadas en la tabla 24.7. Observe
cómo el uso de los siete puntos para caracterizar esta función que varía en forma continua
deja fuera dos picos en x = 2.5 y 12.5 ft.

Subestimados

10
[ (x)]

F(x) cos

Sobreestimados

0
0 30
x, ft
FIGURA 24.7
Representación gráfi ca del porqué la regla del trapecio con dos segmentos da una buena
estimación de la integral en este caso específi co. Casualmente, el uso de dos trapezoides
lleva a un equilibrio entre los errores negativo y positivo.

ran los datos en F(2.5) cos [q(2.5)] = 4.3500 y F(12.5) cos [q(12.5)] = 11.3600, podríamos
determinar una estimación de la integral utilizando el algoritmo para datos irregularmente
espaciados que se describió en la sección 21.3. La figura 24.8 ilustra la segmentación irre-
gular en este caso. Si se incluyen dos puntos adicionales se obtiene una mejor estimación de
= 2.02%). Así, la inclusión de datos adicionales incorporaría los picos
la integral: 126.9 (e t
que antes no se tomaron en cuenta y, en consecuencia, se tendrían mejores resultados.

6/12/06 14:01:16
Chapra-24.indd 692 6/12/06 14:01:16
Chapra-24.indd 692