Page 715 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

24.4 INTEGRACIÓN NUMÉRICA PARA CALCULAR EL TRABAJO 691

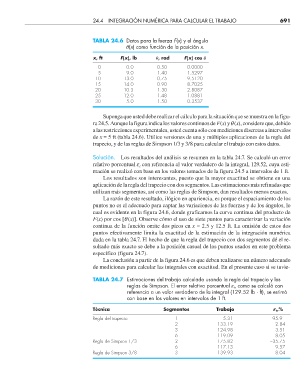
TABLA 24.6 Datos para la fuerza F(x) y el ángulo
q(x) como función de la posición x.

x, ft F(x), lb q, rad F(x) cos q
0 0.0 0.50 0.0000
5 9.0 1.40 1.5297
10 13.0 0.75 9.5120
15 14.0 0.90 8.7025
20 10.5 1.30 2.8087
25 12.0 1.48 1.0881
30 5.0 1.50 0.3537

Suponga que usted debe realizar el cálculo para la situación que se muestra en la figu-
ra 24.5. Aunque la figura indica los valores continuos de F(x) y q(x), considere que, debido
a las restricciones experimentales, usted cuenta sólo con mediciones discretas a intervalos
de x = 5 ft (tabla 24.6). Utilice versiones de una y múltiples aplicaciones de la regla del
trapecio, y de las reglas de Simpson 1/3 y 3/8 para calcular el trabajo con estos datos.

Solución. Los resultados del análisis se resumen en la tabla 24.7. Se calculó un error
con referencia al valor verdadero de la integral, 129.52, cuya esti-
relativo porcentual e t
mación se realizó con base en los valores tomados de la figura 24.5 a intervalos de 1 ft.
Los resultados son interesantes, puesto que la mayor exactitud se obtiene en una
aplicación de la regla del trapecio con dos segmentos. Las estimaciones más refinadas que
utilizan más segmentos, así como las reglas de Simpson, dan resultados menos exactos.
La razón de este resultado, ilógico en apariencia, es porque el espaciamiento de los
puntos no es el adecuado para captar las variaciones de las fuerzas y de los ángulos, lo
cual es evidente en la figura 24.6, donde graficamos la curva continua del producto de
F(x) por cos [q(x)]. Observe cómo el uso de siete puntos para caracterizar la variación
continua de la función omite dos picos en x = 2.5 y 12.5 ft. La omisión de estos dos
puntos efectivamente limita la exactitud de la estimación de la integración numérica
dada en la tabla 24.7. El hecho de que la regla del trapecio con dos segmentos dé el re-
sultado más exacto se debe a la posición casual de los puntos usados en este problema
específico (figura 24.7).
La conclusión a partir de la figura 24.6 es que deben realizarse un número adecuado
de mediciones para calcular las integrales con exactitud. En el presente caso si se tuvie-
TABLA 24.7 Estimaciones del trabajo calculado usando la regla del trapecio y las
reglas de Simpson. El error relativo porcentual e t , como se calculó con
referencia a un valor verdadero de la integral (129.52 lb · ft), se estimó
con base en los valores en intervalos de 1 ft.

Técnica Segmentos Trabajo ε t ,%
Regla del trapecio 1 5.31 95.9
2 133.19 2.84
3 124.98 3.51
6 119.09 8.05
Regla de Simpson 1/3 2 175.82 –35.75
6 117.13 9.57
Regla de Simpson 3/8 3 139.93 –8.04

6/12/06 14:01:16
Chapra-24.indd 691 6/12/06 14:01:16
Chapra-24.indd 691