Page 781 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

25.5 MÉTODOS ADAPTATIVOS DE RUNGE-KUTTA 757

y

1

0 1 2 3 x

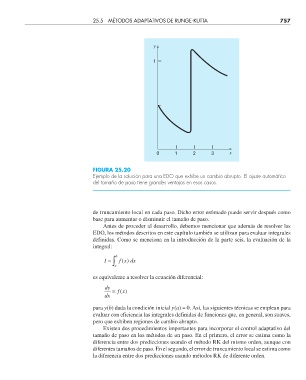
FIGURA 25.20
Ejemplo de la solución para una EDO que exhibe un cambio abrupto. El ajuste automático
del tamaño de paso tiene grandes ventajas en esos casos.

de truncamiento local en cada paso. Dicho error estimado puede servir después como
base para aumentar o disminuir el tamaño de paso.
Antes de proceder al desarrollo, debemos mencionar que además de resolver las
EDO, los métodos descritos en este capítulo también se utilizan para evaluar integrales
definidas. Como se menciona en la introducción de la parte seis, la evaluación de la
integral:

I = ∫ a b f x dx()

es equivalente a resolver la ecuación diferencial:
dy
= fx()
dx

para y(b) dada la condición inicial y(a) = 0. Así, las siguientes técnicas se emplean para
evaluar con eficiencia las integrales definidas de funciones que, en general, son suaves,
pero que exhiben regiones de cambio abrupto.
Existen dos procedimientos importantes para incorporar el control adaptativo del
tamaño de paso en los métodos de un paso. En el primero, el error se estima como la
diferencia entre dos predicciones usando el método RK del mismo orden, aunque con
diferentes tamaños de paso. En el segundo, el error de truncamiento local se estima como
la diferencia entre dos predicciones usando métodos RK de diferente orden.

6/12/06 14:02:05
Chapra-25.indd 757 6/12/06 14:02:05
Chapra-25.indd 757