Page 780 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

756 MÉTODOS DE RUNGE-KUTTA

4 4
y 1
2 2
y
y , y 3 3
1
y 0 y 0

y , y 4
2
–2 –2
y 2 y 4
–4 –4
0 1 2 3 4 0 1 2 3 4
x x

a) b)
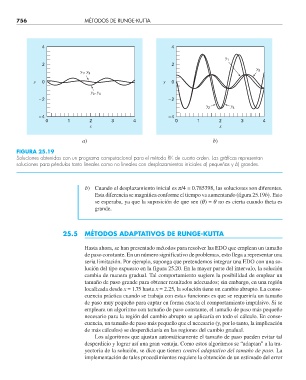
FIGURA 25.19
Soluciones obtenidas con un programa computacional para el método RK de cuarto orden. Las gráfi cas representan
soluciones para péndulos tanto lineales como no lineales con desplazamientos iniciales a) pequeñas y b) grandes.

b) Cuando el desplazamiento inicial es p/4 = 0.785398, las soluciones son diferentes.
Esta diferencia se magnifi ca conforme el tiempo va aumentando (fi gura 25.19b). Esto
se esperaba, ya que la suposición de que sen (q) = q no es cierta cuando theta es
grande.

25.5 MÉTODOS ADAPTATIVOS DE RUNGE-KUTTA

Hasta ahora, se han presentado métodos para resolver las EDO que emplean un tamaño
de paso constante. En un número significativo de problemas, esto llega a representar una
seria limitación. Por ejemplo, suponga que pretendemos integrar una EDO con una so-
lución del tipo expuesto en la figura 25.20. En la mayor parte del intervalo, la solución
cambia de manera gradual. Tal comportamiento sugiere la posibilidad de emplear un
tamaño de paso grande para obtener resultados adecuados; sin embargo, en una región
localizada desde x = 1.75 hasta x = 2.25, la solución tiene un cambio abrupto. La conse-
cuencia práctica cuando se trabaja con estas funciones es que se requeriría un tamaño
de paso muy pequeño para captar en forma exacta el comportamiento impulsivo. Si se
empleara un algoritmo con tamaño de paso constante, el tamaño de paso más pequeño
necesario para la región del cambio abrupto se aplicaría en todo el cálculo. En conse-
cuencia, un tamaño de paso más pequeño que el necesario (y, por lo tanto, la implicación
de más cálculos) se desperdiciaría en las regiones del cambio gradual.
Los algoritmos que ajustan automáticamente el tamaño de paso pueden evitar tal
desperdicio y lograr así una gran ventaja. Como estos algoritmos se “adaptan” a la tra-
yectoria de la solución, se dice que tienen control adaptativo del tamaño de paso. La
implementación de tales procedimientos requiere la obtención de un estimado del error

6/12/06 14:02:05
Chapra-25.indd 756 6/12/06 14:02:05
Chapra-25.indd 756