Page 966 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

942 ESTUDIO DE CASOS: ECUACIONES DIFERENCIALES PARCIALES

las cuales se resuelven para obtener

V = 521.19 V = 421.85 V = 521.19
1,1 2,1 3,1
V = 855.47 V = 755.40 V = 855.47
1,2 2,2 3,2
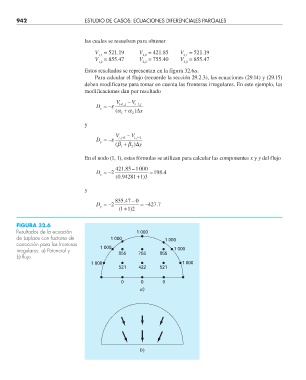
Estos resultados se representan en la figura 32.6a.
Para calcular el flujo (recuerde la sección 29.2.3), las ecuaciones (29.14) y (29.15)
deben modificarse para tomar en cuenta las fronteras irregulares. En este ejemplo, las
modificaciones dan por resultado

V – V
D = –ε i+ ,1 j i– ,1 j
x (α +α )∆
1 2 x
y

V – V
D = –ε ij+, 1 ij , –1
(β 1 + β 2 )∆ y
y
En el nodo (1, 1), estas fórmulas se utilizan para calcular las componentes x y y del flujo
421 .85 1000
–
D = –2 = 198 .4
x
(.0 94281 + )1 3
y
855 .47 0
–
D = –2 = –427 .7
y
(11
+ )2
FIGURA 32.6
Resultados de la ecuación 1 000
de Laplace con factores de 1 000 1 000
corrección para las fronteras
1 000
irregulares. a) Potencial y 855 755 855 1 000
b) fl ujo.
1 000 1 000
521 422 521

0 0 0
a)

b)

6/12/06 14:05:45
Chapra-32.indd 942
Chapra-32.indd 942 6/12/06 14:05:45