Page 14 - FOCUS KSSM TG 4 MATEMATIK TAMBAHAN

Matematik Tambahan Tingkatan 4 Bab 7 Geometri Koordinat

13 Luas PQR
1 3 6 10 3
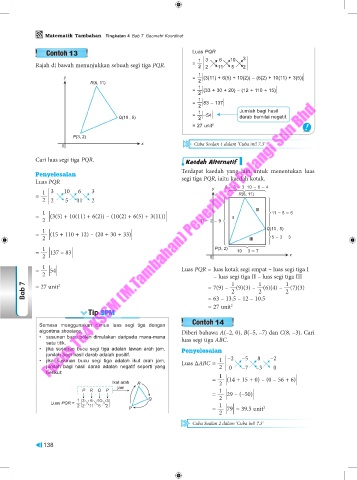
Rajah di bawah menunjukkan sebuah segi tiga PQR. = — 11 5 2
2 2
1
y = —(3(11) + 6(5) + 10(2)) – (6(2) + 10(11) + 3(5))
R(6, 11) 2
1
= —(33 + 30 + 20) – (12 + 110 + 15)
2
1
= —83 – 137
2
1
= —–54 Jumlah bagi hasil
Q(10 , 5) 2 darab bernilai negatif.
= 27 unit 2
P(3, 2)
x Cuba Soalan 1 dalam ‘Cuba ini! 7.3’
0
Cari luas segi tiga PQR. Kaedah Alternatif
Penyelesaian Terdapat kaedah yang lain untuk menentukan luas
Luas PQR segi tiga PQR, iaitu kaedah kotak.
6 3 3 10 6 4
= 1 3 10 6 3 y R(6, 11)
2 2 5 11 2
1 II 11 5 6

= (3(5) + 10(11) + 6(2)) – (10(2) + 6(5) + 3(11))  I
2 11 2 9
1 Q(10 , 5)

= (15 + 110 + 12) – (20 + 30 + 33) 
2 III 5 2 3
1 P(3, 2)

= 137 – 83  10 3 7
2 0 x
1
 
= 54 Luas PQR = luas kotak segi empat – luas segi tiga I
2 – luas segi tiga II – luas segi tiga III
Bab 7 = 27 unit 2 = 7(9) – 1 2 (9)(3) – 1 2 (6)(4) – 1 2 (7)(3)
= 63 – 13.5 – 12 – 10.5
= 27 unit 2
Tip SPM
14
Semasa menggunakan rumus luas segi tiga dengan
algoritma shoelace, Diberi bahawa A(–2, 0), B(–5, –7) dan C(8, –3). Cari
• susunan bucu boleh dimulakan daripada mana-mana luas segi tiga ABC.
satu titik.
• jika susunan bucu segi tiga adalah lawan arah jam, Penyelesaian
jumlah bagi hasil darab adalah positif.
• jika susunan bucu segi tiga adalah ikut arah jam, Luas ΔABC = 1 –2 –5 8 –2
jumlah bagi hasil darab adalah negatif seperti yang 2 0 –7 –3 0
berikut: 1

= (14 + 15 + 0) – (0 – 56 + 6) 
Ikut arah R 2
jam
P R Q P 1

= 29 – (–50) 
1 3 6 10 3 Q 2
Luas PQR = — 1
 
2 2 11 5 2
P = 2 79 = 39.5 unit 2
Cuba Soalan 2 dalam ‘Cuba ini! 7.3’
138