Page 240 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

216 ESTUDIO DE CASOS: RAÍCES DE ECUACIONES

6

4

f (/p) 2

/p
0
1 2
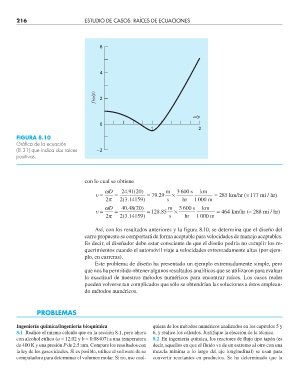
FIGURA 8.10
Gráfi ca de la ecuación
(8.31) que indica dos raíces –2
positivas.

con lo cual se obtiene

v = ωD = 24 91 20.( ) = 79 29. m × 3 600 s km = 285 km/hr (= 177 mi / hr)
2 π 2 3 14159(. ) s hr 1 000 m
v = ωD = 40 48 20.( ) = 128 85. m × 3 600 s km = 464 km/hr (= 288 mi / hr)
2 π 2 3 14159(. ) s hr 1 000 m

Así, con los resultados anteriores y la figura 8.10, se determina que el diseño del
carro propuesto se comportará de forma aceptable para velocidades de manejo aceptables.
Es decir, el diseñador debe estar consciente de que el diseño podría no cumplir los re-
querimientos cuando el automóvil viaje a velocidades extremadamente altas (por ejem-
plo, en carreras).
Este problema de diseño ha presentado un ejemplo extremadamente simple, pero
que nos ha permitido obtener algunos resultados analíticos que se utilizaron para evaluar
la exactitud de nuestros métodos numéricos para encontrar raíces. Los casos reales
pueden volverse tan complicados que sólo se obtendrían las soluciones a éstos emplean-
do métodos numéricos.

PROBLEMAS

Ingeniería química/Ingeniería bioquímica quiera de los métodos numéricos analizados en los capítulos 5 y
8.1 Realice el mismo cálculo que en la sección 8.1, pero ahora 6, y realice los cálculos. Justifique la elección de la técnica.
con alcohol etílico (a = 12.02 y b = 0.08407) a una temperatura 8.2 En ingeniería química, los reactores de flujo tipo tapón (es
de 400 K y una presión P de 2.5 atm. Compare los resultados con decir, aquellos en que el fluido va de un extremo al otro con una
la ley de los gases ideales. Si es posible, utilice el software de su mezcla mínima a lo largo del eje longitudinal) se usan para
computadora para determinar el volumen molar. Si no, use cual- convertir reactantes en productos. Se ha determinado que la

6/12/06 13:51:56
Chapra-08.indd 216 6/12/06 13:51:56
Chapra-08.indd 216