Page 481 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

PT5.2 ANTECEDENTES MATEMÁTICOS 457

5

4
Frecuencia 3

2

1

0
6.4 6.6 6.8

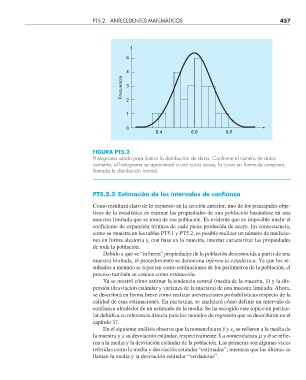
FIGURA PT5.2
Histograma usado para ilustrar la distribución de datos. Conforme el número de datos
aumenta, el histograma se aproximará a una curva suave, la curva en forma de campana,
llamada la distribución normal.

PT5.2.3 Estimación de los intervalos de confi anza
Como resultará claro de lo expuesto en la sección anterior, uno de los principales obje-
tivos de la estadística es estimar las propiedades de una población basándose en una
muestra limitada que se toma de esa población. Es evidente que es imposible medir el
coeficiente de expansión térmica de cada pieza producida de acero. En consecuencia,
como se muestra en las tablas PT5.1 y PT5.2, es posible realizar un número de medicio-
nes en forma aleatoria y, con base en la muestra, intentar caracterizar las propiedades
de toda la población.
Debido a que se “infieren” propiedades de la población desconocida a partir de una
muestra limitada, el procedimiento se denomina inferencia estadística. Ya que los re-
sultados a menudo se reportan como estimaciones de los parámetros de la población, el
proceso también se conoce como estimación.
–
Ya se mostró cómo estimar la tendencia central (media de la muestra, y) y la dis-
persión (desviación estándar y varianza de la muestra) de una muestra limitada. Ahora,
se describirá en forma breve cómo realizar aseveraciones probabilísticas respecto de la
calidad de esas estimaciones. En particular, se analizará cómo definir un intervalo de
confianza alrededor de un estimado de la media. Se ha escogido este tópico en particu-
lar debido a su relevancia directa para los modelos de regresión que se describirán en el
capítulo 17.
–
En el siguiente análisis observe que la nomenclatura y y s y se refieren a la media de
la muestra y a su desviación estándar, respectivamente. La nomenclatura m y s se refie-
ren a la media y la desviación estándar de la población. Las primeras son algunas veces
referidas como la media y desviación estándar “estimadas”; mientras que las últimas se
llaman la media y la desviación estándar “verdaderas”.

6/12/06 13:57:08
Chapra-17.indd 457 6/12/06 13:57:08
Chapra-17.indd 457