Page 482 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

458 AJUSTE DE CURVAS

Distribución de las
–
medias de y, y

1–

/2 /2
y
a)
L – U
– z
b)
z – /2 –1 0 1 z /2

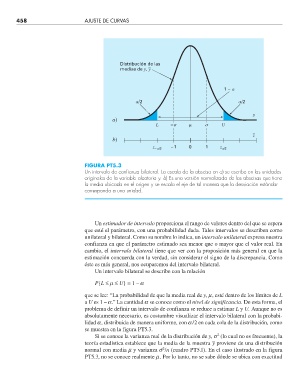
FIGURA PT5.3
Un intervalo de confi anza bilateral. La escala de la abscisa en a) se escribe en las unidades
originales de la variable aleatoria y. b) Es una versión normalizada de las abscisas que tiene
la media ubicada en el origen y se escala el eje de tal manera que la desviación estándar
corresponda a una unidad.

Un estimador de intervalo proporciona el rango de valores dentro del que se espera
que esté el parámetro, con una probabilidad dada. Tales intervalos se describen como
unilateral y bilateral. Como su nombre lo indica, un intervalo unilateral expresa nuestra
confianza en que el parámetro estimado sea menor que o mayor que el valor real. En
cambio, el intervalo bilateral tiene que ver con la proposición más general en que la
estimación concuerda con la verdad, sin considerar el signo de la discrepancia. Como
éste es más general, nos ocuparemos del intervalo bilateral.
Un intervalo bilateral se describe con la relación
P{L ≤ m ≤ U} = 1 – a

que se lee: “La probabilidad de que la media real de y, m, esté dentro de los límites de L
a U es 1 – a.” La cantidad a se conoce como el nivel de significancia. De esta forma, el
problema de definir un intervalo de confianza se reduce a estimar L y U. Aunque no es
absolutamente necesario, es costumbre visualizar el intervalo bilateral con la probabi-
lidad a, distribuida de manera uniforme, con a/2 en cada cola de la distribución, como
se muestra en la figura PT5.3.
2
Si se conoce la varianza real de la distribución de y, s (lo cual no es frecuente), la
–
teoría estadística establece que la media de la muestra y proviene de una distribución
2
normal con media m y varianza s /n (cuadro PT5.1). En el caso ilustrado en la figura
PT5.3, no se conoce realmente m. Por lo tanto, no se sabe dónde se ubica con exactitud

6/12/06 13:57:09
Chapra-17.indd 458 6/12/06 13:57:09
Chapra-17.indd 458