Page 674 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

650 INTEGRACIÓN DE ECUACIONES

100

10 1

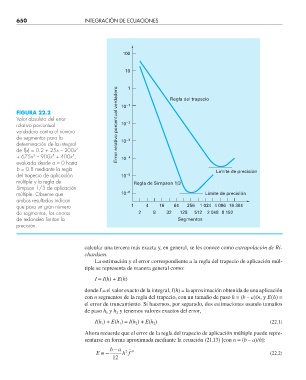
FIGURA 22.2 10 –1 Regla del trapecio
Valor absoluto del error
relativo porcentual Error relativo porcentual verdadero 10 –2
verdadero contra el número
de segmentos para la –3
determinación de la integral 10
2
de f(x) = 0.2 + 25x – 200x
3
4
5
+ 675x – 900x + 400x , 10 –4
evaluada desde a = 0 hasta
b = 0.8 mediante la regla Límite de precisión
del trapecio de aplicación 10 –5
múltiple y la regla de Regla de Simpson 1/3
Simpson 1/3 de aplicación
múltiple. Observe que 10 –6 Límite de precisión
ambos resultados indican
que para un gran número 1 4 16 64 256 1 024 4 096 16 384
de segmentos, los errores 2 8 32 128 512 2 048 8 192
de redondeo limitan la Segmentos
precisión.

calcular una tercera más exacta y, en general, se les conoce como extrapolación de Ri-
chardson.
La estimación y el error correspondiente a la regla del trapecio de aplicación múl-
tiple se representa de manera general como:
I = I(h) + E(h)

donde I = el valor exacto de la integral, I(h) = la aproximación obtenida de una aplicación
con n segmentos de la regla del trapecio, con un tamaño de paso h = (b – a)/n, y E(h) =
el error de truncamiento. Si hacemos, por separado, dos estimaciones usando tamaños
y h y tenemos valores exactos del error,
de paso h 1 2
I(h ) + E(h ) = I(h ) + E(h ) (22.1)
2
1
1
2
Ahora recuerde que el error de la regla del trapecio de aplicación múltiple puede repre-
sentarse en forma aproximada mediante la ecuación (21.13) [con n = (b – a)/h]:
ba−
E ≅− hf ′′ (22.2)
2
12

6/12/06 14:00:18
Chapra-22.indd 650 6/12/06 14:00:18
Chapra-22.indd 650