Page 680 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

656 INTEGRACIÓN DE ECUACIONES

f (x)

x
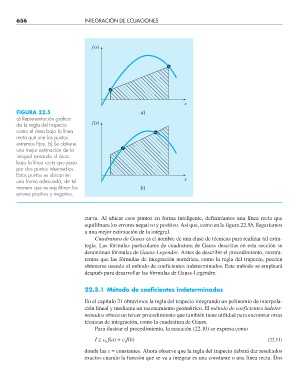
FIGURA 22.5 a)
a) Representación gráfi ca
de la regla del trapecio f (x)
como el área bajo la línea
recta que une los puntos
extremos fi jos. b) Se obtiene
una mejor estimación de la
integral tomando el área
bajo la línea recta que pasa
por dos puntos intermedios.
Estos puntos se ubican en
una forma adecuada, de tal x
manera que se equilibran los b)
errores positivo y negativo.

curva. Al ubicar esos puntos en forma inteligente, definiríamos una línea recta que
equilibrara los errores negativo y positivo. Así que, como en la figura 22.5b, llegaríamos
a una mejor estimación de la integral.
Cuadratura de Gauss es el nombre de una clase de técnicas para realizar tal estra-
tegia. Las fórmulas particulares de cuadratura de Gauss descritas en esta sección se
denominan fórmulas de Gauss-Legendre. Antes de describir el procedimiento, mostra-
remos que las fórmulas de integración numérica, como la regla del trapecio, pueden
obtenerse usando el método de coeficientes indeterminados. Este método se empleará
después para desarrollar las fórmulas de Gauss-Legendre.

22.3.1 Método de coefi cientes indeterminados

En el capítulo 21 obtuvimos la regla del trapecio integrando un polinomio de interpola-
ción lineal y mediante un razonamiento geométrico. El método de coeficientes indeter-
minados ofrece un tercer procedimiento que también tiene utilidad para encontrar otras
técnicas de integración, como la cuadratura de Gauss.
Para ilustrar el procedimiento, la ecuación (22.10) se expresa como

I ≅ c f(a) + c f(b) (22.11)
0
1
donde las c = constantes. Ahora observe que la regla del trapecio deberá dar resultados
exactos cuando la función que se va a integrar es una constante o una línea recta. Dos

6/12/06 14:00:20
Chapra-22.indd 656 6/12/06 14:00:20
Chapra-22.indd 656