Page 682 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

658 INTEGRACIÓN DE ECUACIONES

y
ba ba
–
–
−c 0 + c 1 = 0
2 2
Éstas son dos ecuaciones con dos incógnitas que se resuelven para encontrar
–
ba
c = c =
0
1
2
que, al sustituirse en la ecuación (22.11), da
ba– ba–
I = fa +() fb()
2 2
que es equivalente a la regla del trapecio.

22.3.2 Desarrollo de la fórmula de Gauss-Legendre
de dos puntos

Así como en el caso anterior para la obtención de la regla del trapecio, el objetivo de la
cuadratura de Gauss es determinar los coeficientes de una ecuación de la forma

I ≅ c 0 f(x 0 ) + c 1 f(x 1 ) (22.12)
donde las c = los coeficientes desconocidos. Sin embargo, a diferencia de la regla del
trapecio que utiliza puntos extremos fijos a y b, los argumentos de la función x 0 y x 1 no
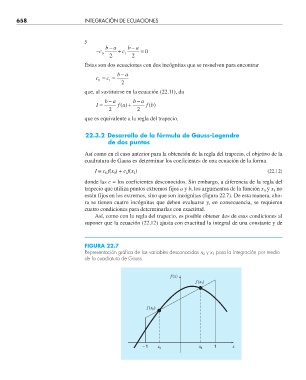
están fijos en los extremos, sino que son incógnitas (figura 22.7). De esta manera, aho-
ra se tienen cuatro incógnitas que deben evaluarse y, en consecuencia, se requieren
cuatro condiciones para determinarlas con exactitud.
Así, como con la regla del trapecio, es posible obtener dos de esas condiciones al
suponer que la ecuación (22.12) ajusta con exactitud la integral de una constante y de

FIGURA 22.7
Representación gráfi ca de las variables desconocidas x 0 y x 1 para la integración por medio
de la cuadratura de Gauss.

f(x)
f(x )
1

f(x )
0

–1 x 0 x 1 1 x

6/12/06 14:00:20
Chapra-22.indd 658
Chapra-22.indd 658 6/12/06 14:00:20