Page 689 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

22.4 INTEGRALES IMPROPIAS 665

N(x)= 1 1 e –x 2 /2 dx

– 2

a)
– y –2s y – y – s y – y – y + s y – y +2s y y

b)
–3 –2 –1 0 1 2 3 x
N(x)
1

N(x)= 1
0.5 1 e –x 2 /2 dx
– 2

c)
–3 –2 –1 0 1 2 3 x

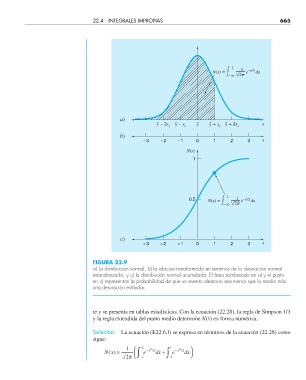
FIGURA 22.9
a) La distribución normal, b) la abscisa transformada en términos de la desviación normal
estandarizada, y c) la distribución normal acumulada. El área sombreada en a) y el punto
en c) representan la probabilidad de que un evento aleatorio sea menor que la media más
una desviación estándar.

te y se presenta en tablas estadísticas. Con la ecuación (22.28), la regla de Simpson 1/3
y la regla extendida del punto medio determine N(1) en forma numérica.

Solución. La ecuación (E22.6.1) se expresa en términos de la ecuación (22.28) como
sigue:
1 ⎛ –2 2 1 2 ⎞
Nx() = ⎝∫ e – x /2 dx + ∫ e – x /2 dx
2π –∞ –2 ⎠

6/12/06 14:00:22
Chapra-22.indd 665 6/12/06 14:00:22
Chapra-22.indd 665