Page 711 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

24.3 RAÍZ MEDIA CUADRÁTICA DE LA CORRIENTE 687

Por lo tanto, a partir de la ecuación (24.9):

T = V = 6 440 .6 = 6 473 lb
cosθ . 0 995

y de la ecuación (24.8):
H = F – T sen q = 1 480.6 – (6 473)(0.0995) = 836.54 lb

Ahora al conocer estas fuerzas nos permite continuar con otros aspectos del diseño es-
tructural del bote, tales como los cables y el sistema de soporte del mástil en la cubierta.
Este problema ilustra claramente dos usos de la integración numérica que pueden en-
contrarse en el diseño de estructuras en ingeniería. Se ve que ambas reglas, la del trape-
cio y la de Simpson 1/3, son fáciles de aplicar y constituyen herramientas prácticas en
la solución de problemas. La regla de Simpson 1/3 es más exacta que la del trapecio para
el mismo tamaño de paso, por lo que a menudo se prefiere aquélla.

24.3 RAÍZ MEDIA CUADRÁTICA DE LA CORRIENTE MEDIANTE
INTEGRACIÓN NUMÉRICA (INGENIERÍA ELÉCTRICA)

Antecedentes. El valor promedio de una corriente eléctrica oscilante en un periodo
puede ser cero. Por ejemplo, suponga que la corriente se describe por una senoide simple:
i(t) = sen (2p/T), donde T es el periodo. El valor promedio de esta función se determina
mediante la siguiente ecuación:

∫ T sen ⎛ 2π t ⎞ dt
2π)
i = 0 ⎝ T ⎠ = – cos ( + cos 0 = 0
T 0 T
–

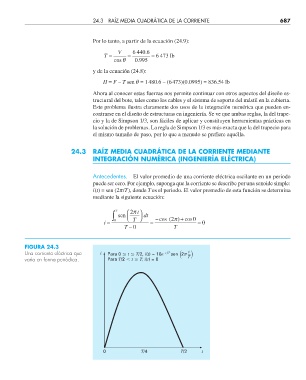
FIGURA 24.3

Una corriente eléctrica que i Para 0 t T/2, i(t)=10e –t /T sen 2 t
varía en forma periódica. Para T/2 t T, i(t)=0 T

0 T/4 T/2 t

6/12/06 14:01:15
Chapra-24.indd 687 6/12/06 14:01:15
Chapra-24.indd 687