Page 792 - Chapra y Canale. Metodos Numericos para Ingenieros 5edición_Neat

768 MÉTODOS RÍGIDOS Y DE PASOS MÚLTIPLES

y
3

2
1

1
0
0 0.01 0.02

0
0 2 4 x

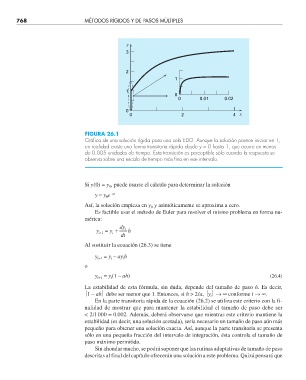
FIGURA 26.1
Gráfi ca de una solución rígida para una sola EDO. Aunque la solución parece iniciar en 1,
en realidad existe una forma transitoria rápida desde y = 0 hasta 1, que ocurre en menos
de 0.005 unidades de tiempo. Esta transición es perceptible sólo cuando la respuesta se
observa sobre una escala de tiempo más fi na en ese intervalo.

Si y(0) = y , puede usarse el cálculo para determinar la solución
0
y = y e –at
0
Así, la solución empieza en y y asintóticamente se aproxima a cero.
0
Es factible usar el método de Euler para resolver el mismo problema en forma nu-
mérica:

y i+1 = y + dy i h
i
dt
Al sustituir la ecuación (26.3) se tiene
y = y – ay h
i
i+1
i
o
y = y (1 – ah) (26.4)
i
i+1
La estabilidad de esta fórmula, sin duda, depende del tamaño de paso h. Es decir,
⏐ → ∞ conforme i → ∞.
⏐1 – ah⏐ debe ser menor que 1. Entonces, si h > 2/a, ⏐y i
En la parte transitoria rápida de la ecuación (26.2) se utiliza este criterio con la fi-
nalidad de mostrar que para mantener la estabilidad el tamaño de paso debe ser
< 2/1 000 = 0.002. Además, deberá observarse que mientras este criterio mantiene la
estabilidad (es decir, una solución acotada), sería necesario un tamaño de paso aún más
pequeño para obtener una solución exacta. Así, aunque la parte transitoria se presenta
sólo en una pequeña fracción del intervalo de integración, ésta controla el tamaño de
paso máximo permitido.
Sin ahondar mucho, se podrá suponer que las rutinas adaptativas de tamaño de paso
descritas al final del capítulo ofrecerán una solución a este problema. Quizá pensará que

6/12/06 14:02:30
Chapra-26.indd 768
Chapra-26.indd 768 6/12/06 14:02:30